题目内容
10.若向量$\overrightarrow a=({1,0}),\overrightarrow b=({2,1}),\overrightarrow c=({x,1})$满足$({3\overrightarrow a-\overrightarrow b})⊥\overrightarrow c$,则x=1.分析 由已知向量的坐标求出$3\overrightarrow{a}-\overrightarrow{b}$的坐标,再由$({3\overrightarrow a-\overrightarrow b})⊥\overrightarrow c$列式求得x值.
解答 解:∵$\overrightarrow{a}=(1,0),\overrightarrow{b}=(2,1)$,
∴$3\overrightarrow{a}-\overrightarrow{b}=(1,-1)$,又$\overrightarrow{c}=(x,1)$,且$({3\overrightarrow a-\overrightarrow b})⊥\overrightarrow c$,
∴x-1=0,即x=1.
故答案为:1.
点评 本题考查平面向量的数量积运算,考查了向量垂直与坐标之间的关系,是基础的计算题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
18.已知幂函数f(x)=xn的图象过点(8,$\frac{1}{4}$),且f(a+1)<f(2),则a的范围是( )
| A. | -3<a<1 | B. | a<-3或a>1 | C. | a<1 | D. | a>1 |
5.原命题为“若两条直线的斜率相等,则这两条直线平行”,关于其逆命题、否命题、逆否命题真假性的判断依次如下,正确的是( )
| A. | 真、假、真 | B. | 假、假、真 | C. | 真、真、假 | D. | 假、假、假 |
20.执行如图所示程序框图,若输出的S值为-20,则条件框内应填写( )


| A. | i>3? | B. | i<4? | C. | i>4? | D. | i<5? |
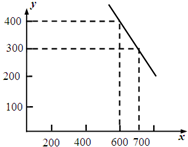 某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).
某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).