题目内容
已知双曲线x2-ky2=1的一个焦点是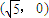 ,则其渐近线方程为 .
,则其渐近线方程为 .
【答案】分析:根据双曲线方程,得a2=1,b2= ,结合题意得c=
,结合题意得c= =
= ,解出k=
,解出k= ,从而得到双曲线方程,由此不难得出该双曲线的渐近线方程.
,从而得到双曲线方程,由此不难得出该双曲线的渐近线方程.
解答:解:双曲线x2-ky2=1化成标准方程得x2- =1,
=1,
得a2=1,b2= ,
,
∴c=
∵双曲线的一个焦点是( ,0),
,0),
∴ =
= ,解之得k=
,解之得k= ,双曲线方程为x2-
,双曲线方程为x2- =1,
=1,
得a=1,b=2
∴该双曲线的渐近线方程为y=± x,即y=±2x
x,即y=±2x
故答案为:y=±2x.
点评:本题给出含有参数的双曲线方程,在已知其一个焦点的情况下求双曲线的渐近线方程,着重考查了双曲线的标准方程与简单几何性质等知识,属于基础题.
 ,结合题意得c=
,结合题意得c= =
= ,解出k=
,解出k= ,从而得到双曲线方程,由此不难得出该双曲线的渐近线方程.
,从而得到双曲线方程,由此不难得出该双曲线的渐近线方程.解答:解:双曲线x2-ky2=1化成标准方程得x2-
 =1,
=1,得a2=1,b2=
 ,
,∴c=

∵双曲线的一个焦点是(
 ,0),
,0),∴
 =
= ,解之得k=
,解之得k= ,双曲线方程为x2-
,双曲线方程为x2- =1,
=1,得a=1,b=2
∴该双曲线的渐近线方程为y=±
 x,即y=±2x
x,即y=±2x故答案为:y=±2x.
点评:本题给出含有参数的双曲线方程,在已知其一个焦点的情况下求双曲线的渐近线方程,着重考查了双曲线的标准方程与简单几何性质等知识,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 ,则其渐近线方程为 .
,则其渐近线方程为 . ),则其离心率为 .
),则其离心率为 .