题目内容
已知函数![]() 。
。
(Ⅰ)当![]() 时,利用函数单调性的定义判断并证明
时,利用函数单调性的定义判断并证明![]() 的单调性,并求其值域;
的单调性,并求其值域;
(Ⅱ)若对任意![]() ,求实数a的取值范围。
,求实数a的取值范围。
解析:(Ⅰ)任取![]()
则![]()
![]()
![]() ,……………………………………………………2分
,……………………………………………………2分
当![]()
∵![]() ∴
∴![]() ,恒成立
,恒成立
∴![]()
∴![]() 上是增函数,
上是增函数,
∴当x=1时,f(x)取得最小值为![]() ,
,
∴f(x)的值域为![]()
(Ⅱ)![]() ,
,
∵对任意![]() ,恒成立
,恒成立
∴只需对任意![]() 恒成立。
恒成立。
设![]()
∵g(x)的对称轴为x=-1, ∴只需g(1)>0便可, g(1)=3+a>0,
∴a>-3。
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
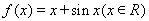
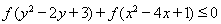


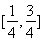
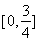

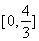
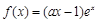 ,
,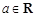
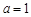 时,求函数
时,求函数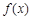 的极值;
的极值;
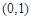 上是单调增函数,求实数
上是单调增函数,求实数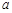 的取值范围.
的取值范围.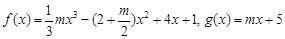 .
. 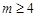 时,求函数
时,求函数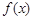 的单调递增区间;
的单调递增区间;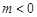 ,使得对任意的
,使得对任意的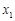 ,
,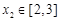 都有
都有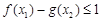 ,若存在,求
,若存在,求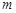 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.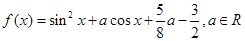 .
.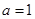 时,求函数
时,求函数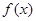 的最大值;
的最大值;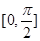 上的任意一个
上的任意一个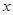 ,都有
,都有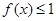 成立,求实数
成立,求实数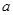 的取值范围.
的取值范围.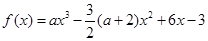 。
。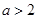 时,求函数
时,求函数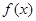 的极小值;
的极小值; 零点的个数。
零点的个数。