题目内容
(本题满分12分)已知函数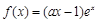 ,
,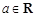
(I)当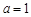 时,求函数
时,求函数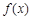 的极值;
的极值;
(II)若函数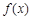 在区间
在区间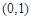 上是单调增函数,求实数
上是单调增函数,求实数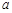 的取值范围.
的取值范围.
【答案】
(I)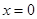 时,
时,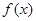 取得极小值
取得极小值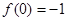 .
.
(II)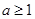
【解析】解:(I)因为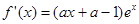 , 所以当
, 所以当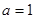 时,
时,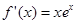 ,
,
令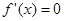 ,则
,则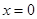 ,所以
,所以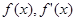 的变化情况如下表:
的变化情况如下表:
|
|
|
0 |
|
|
|
|
0 |
+ |
|
|
|
极小值 |
|
所以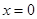 时,
时,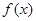 取得极小值
取得极小值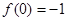 . …………………………………6分
. …………………………………6分
(II) 因为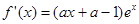 ,函数
,函数 在区间
在区间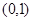 上是单调增函数,
上是单调增函数,
所以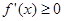 对
对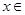
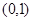 恒成立.又
恒成立.又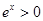 ,所以只要
,所以只要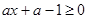 对
对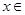
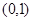 恒成立, 解法一:设
恒成立, 解法一:设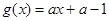 ,则要使
,则要使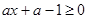 对
对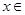
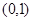 恒成立,
恒成立,
只要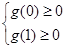 成立,即
成立,即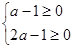 ,解得
,解得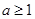 .
.
解法二:要使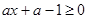 对
对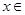
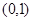 恒成立,
恒成立,
因为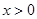 ,所以
,所以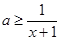 对
对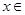
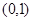 恒成立 ,
恒成立 ,
因为函数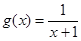 在
在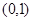 上单调递减,
上单调递减,
所以只要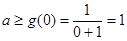 .
.

练习册系列答案
相关题目
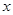
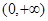
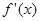

 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围