题目内容
【题目】已知椭圆![]() (
(![]() 为常数且
为常数且![]() )与直线
)与直线![]() 有且只有一个公共点
有且只有一个公共点![]() ,
,![]() .
.
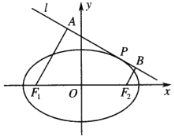
(Ⅰ)当点![]() 的坐标为
的坐标为![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅱ)过椭圆![]() 的两焦点
的两焦点![]() ,
,![]() 作直线
作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,
,![]() ,求四边形
,求四边形![]() 面积的最大值(用
面积的最大值(用![]() 表示).
表示).
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]() ;
;
【解析】
(Ⅰ)首先根据点![]() 在椭圆上求出
在椭圆上求出![]() 的值,然后联立椭圆与直线
的值,然后联立椭圆与直线![]() 的方程,利用
的方程,利用![]() 和点
和点![]() 在直线
在直线![]() 上求得
上求得![]() ,
,![]() 的值即可求解;
的值即可求解;
(Ⅱ)联立椭圆与直线![]() 的方程,然后利用判别式求得
的方程,然后利用判别式求得![]() 的取值范围,再利用点到直线的距离公式求得原点到直线
的取值范围,再利用点到直线的距离公式求得原点到直线![]() 的距离
的距离![]() ,利用三角函数求得
,利用三角函数求得![]() ,从而得到四边形
,从而得到四边形![]() 的面积的表达式,然后通过构造函数,利用函数的单调性即可求得最大值.
的面积的表达式,然后通过构造函数,利用函数的单调性即可求得最大值.
(Ⅰ)已知点![]() 在椭圆
在椭圆![]() 上,所以得出
上,所以得出![]() .
.
由椭圆![]() 的方程
的方程![]() 与直线
与直线![]() 联立,
联立,
可得![]() ,
,
因为此方程有且只有一解为![]() ,
,
所以![]() ,
,
又![]() ,解得
,解得![]() ,
,![]() ,
,
从而得直线![]() 的方程为
的方程为![]() .
.
(Ⅱ)由椭圆![]() 与直线
与直线![]() 联立,
联立,
可得![]() ,
,
由![]() 可得
可得![]() ,
,
由![]() ,
,![]() 可知,
可知,![]() ,
,
原点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
![]() ,
,
因为线段![]() 在直线
在直线![]() 上的投影
上的投影![]() ,
,
所以四边形![]() 的面积
的面积![]() ,
,
把![]() 代入可得
代入可得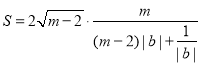 .
.
令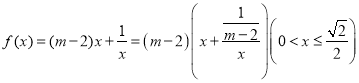 ,
,
由对勾函数的单调性可知,函数![]() 在
在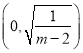 上递减,在
上递减,在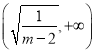 上递增,
上递增,
(ⅰ)当![]() 时,函数
时,函数![]() 在
在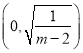 上递减,在
上递减,在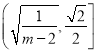 上递增,所以当
上递增,所以当![]() ,四边形
,四边形![]() 的面积
的面积![]() 取得最大值为
取得最大值为![]() ;
;
(ⅱ)当![]() 时,函数
时,函数![]() 在
在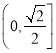 上递减,所以当
上递减,所以当![]() ,四边形
,四边形![]() 的面积
的面积![]() 取得最大值为
取得最大值为![]() .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】2019年郑开国际马拉松比赛,于2019年3月31日在郑州、开封举行.某学校本着“我运动,我快乐,我锻炼,我提高”精神,积极组织学生参加比赛及相关活动,为了了解学生的参与情况,从全校学生中随机抽取了150名学生,对是否参与的情况进行了问卷调查,统计数据如下:
会参与 | 不会参与 | |
男生 | 60 | 40 |
女生 | 20 | 30 |
(1)根据上表说明,能否有97.5%的把握认为参与马拉松赛事与性别有关?
(2)现从参与问卷调查且参与赛事的学生中,采用按性别分层抽样的方法选取8人参加2019年马拉松比赛志愿者宣传活动,
①求男、女学生各选取多少人;
②若从这8人中随机选取2人到校广播站开展2019年赛事宣传介绍,求恰好选到2名男生的概率.
附:参考公式:![]() ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |