Question

【题目】设点M是棱长为2的正方体ABCD-A1B1C1D1的棱AD的中点，点P在面BCC1B1所在的平面内，若平面D1PM分别与平面ABCD和平面BCC1B1所成的锐二面角相等，则点P到点C1的最短距离是（ ）

A.B.C.1D.

Answer 1

【答案】A

【解析】

过点作的平行线交于点、交于点，连接，则是平面与平面的交线，是平面与平面的交线，与平行，交于点，过点作垂直于点，推导出点一定是的中点，从而点到点的最短距离是点到直线的距离，以为原点，为轴，为轴，为轴，建立空间直角坐标系，利用向量法能求出点到点的最短距离．

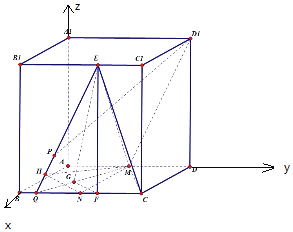
如图，过点作的平行线交于点、交于点，连接，

则是平面与平面的交线，是平面与平面的交线．

与平行，交于点，过点作垂直于点，则有，与平面垂直，

所以，与垂直，即角是平面与平面的夹角的平面角，且，

与平行交于点，过点作垂直于点，

同上有：，且有，又因为，故，

而，故，

而四边形一定是平行四边形，故它还是菱形，即点一定是的中点，

点到点的最短距离是点到直线的距离，

以为原点，为轴，为轴，为轴，建立空间直角坐标系，

，， ，

， ，

点到点的最短距离：

．

故选：．