Question

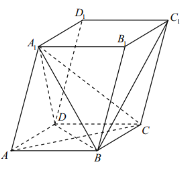
【题目】如图，在四棱锥中，底面是矩形，，，底面.

（1）当为何值时，平面？证明你的结论；

（2）若在边上至少存在一点，使，求的取值范围.

Answer 1

【答案】（1），证明见详解；（2）

【解析】

（1）要证平面，只需证垂直于平面内的两条相交直线，由题意可知，则只需证明，只有当四边形为正方形时满足.

（2）由题意可知，若存在点，使，则平面，即，则点应是以为直径的圆和边的一个公共点，即半径，求解即可.

（1）当时，四边形为正方形，则.

因为平面，平面，

所以，

又，平面，平面

所以平面.

故当时，平面.

（2）设是符合条件的边上的点.

因为平面，平面

所以，

又，，平面，平面

所以平面，

因为平面，

所以.

因此，点应是以为直径的圆和边的一个公共点.

则半径， 即.

所以.