题目内容
已知奇函数f(x)满足f(x+2)=f(x),当x∈(0,1)时,函数f(x)=2x,则f( )=________
)=________
-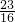
分析:由函数是奇函数得到f(-x)=-f(x)和f(x+2)=f(x)把则f( )进行变形得到
)进行变形得到 ∈(0,1)时函数f(x)=2x,求出即可.
∈(0,1)时函数f(x)=2x,求出即可.
解答:根据对数函数的图象可知 <0,且
<0,且 =-log223;
=-log223;
奇函数f(x)满足f(x+2)=f(x)和f(-x)=-f(x)
则f( )=f(-log223)=-f(log223)=-f(log223-4)=-f(
)=f(-log223)=-f(log223)=-f(log223-4)=-f( ),
),
因为 ∈(0,1)=-
∈(0,1)=- =-
=-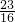
故答案为-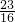
点评:考查学生应用函数奇偶性的能力,函数的周期性的掌握能力,以及运用对数的运算性质能力.
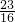
分析:由函数是奇函数得到f(-x)=-f(x)和f(x+2)=f(x)把则f(
 )进行变形得到
)进行变形得到 ∈(0,1)时函数f(x)=2x,求出即可.
∈(0,1)时函数f(x)=2x,求出即可.解答:根据对数函数的图象可知
 <0,且
<0,且 =-log223;
=-log223;奇函数f(x)满足f(x+2)=f(x)和f(-x)=-f(x)
则f(
 )=f(-log223)=-f(log223)=-f(log223-4)=-f(
)=f(-log223)=-f(log223)=-f(log223-4)=-f( ),
),因为
 ∈(0,1)=-
∈(0,1)=- =-
=-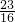
故答案为-
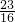
点评:考查学生应用函数奇偶性的能力,函数的周期性的掌握能力,以及运用对数的运算性质能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目