题目内容
20.已知函数y=$\sqrt{3}$cos(2x-$\frac{π}{6}$)+2,求:(1)函数最大值及取得最大值时对应的x的集合;
(2)图象的对称中心和对称轴方程.
分析 (1)根据余弦函数的图象与性质求出函数y的最大值以及取得最大值时x的集合;
(2)由余弦函数的图象与性质求出函数y图象的对称中心和对称轴方程.
解答 解:(1)由函数y=$\sqrt{3}$cos(2x-$\frac{π}{6}$)+2,
令2x-$\frac{π}{6}$=2kπ,k∈Z,
解得x=$\frac{π}{12}$+kπ,k∈Z,
此时函数y取得最大值为$\sqrt{3}$×1+2=$\sqrt{3}$+2;
且y取得最大值时x的集合为{x|x=$\frac{π}{12}$+kπ,k∈Z};
(2)由函数y=$\sqrt{3}$cos(2x-$\frac{π}{6}$)+2,
令2x-$\frac{π}{6}$=$\frac{π}{2}$+kπ,k∈Z,
解得x=$\frac{π}{3}$+$\frac{kπ}{2}$,k∈Z,
∴函数y图象的对称中心为($\frac{π}{3}$+$\frac{kπ}{2}$,0),k∈Z;
令2x-$\frac{π}{6}$=kπ,k∈Z,
解得x=$\frac{π}{12}$+$\frac{kπ}{2}$,k∈Z,
∴函数y的对称轴方程为x=$\frac{π}{12}$+$\frac{kπ}{2}$,k∈Z.
点评 本题考查了余弦函数的图象与性质的应用问题,是基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
8.在等比数列{an}中,S3=1,S6=4,则a10+a11+a12的值是( )
| A. | 81 | B. | 64 | C. | 32 | D. | 27 |
5.已知数列{an},满足a1=-$\frac{1}{2}$,$\frac{{a}_{n}-{a}_{n+1}}{{a}_{n+1}{a}_{n}}$=$\frac{2}{{n}^{2}+n}$,则数列{an}的前n项和的最大值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
12.已知全集U=R,集合$A=\{x|x(x-5)≥0\},B=\{x|y=\sqrt{3-x}\}$,则(∁UA)∩B等于( )
| A. | (0,3) | B. | (0,5) | C. | ∅ | D. | (0,3] |
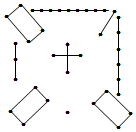 洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.
洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.