题目内容
已知f(x)=asin2x+bcos2x,其中a,b∈R,ab≠0,若f(x)≤|f( )|对一切x∈R恒成立,且f(
)|对一切x∈R恒成立,且f( )>0,则f(x)的单调递增区间是( )
)>0,则f(x)的单调递增区间是( )
A.[kπ- ,kπ+ ,kπ+ ](k∈Z) ](k∈Z) | B.[kπ+ ,kπ+ ,kπ+ ](k∈Z) ](k∈Z) |
C.[kπ,kπ+ ](k∈Z) ](k∈Z) | D.[kπ- ,kπ](k∈Z) ,kπ](k∈Z) |
B
解析试题分析:根据题意,可得 ,(其中
,(其中 ),
), 对一切
对一切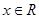 恒成立,
恒成立, 当
当 时,函数有最大值
时,函数有最大值 或最小值
或最小值 ,因此
,因此 ,解得
,解得 ,
,
 ,
, ,从而取
,从而取 得到
得到 ,由此可得
,由此可得 ,令
,令 ,得
,得 ,
, ,
, 的单调递增区间是
的单调递增区间是 .
.
考点:三角函数的最值.

练习册系列答案
相关题目
若函数 (
(
 ),又
),又 ,
, ,且
,且 的最小值为
的最小值为 ,则正数
,则正数 的值是( )
的值是( )
A. | B.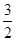 | C. | D. |
函数 的值域为
的值域为
A. | B. | C. | D. |
函数 的部分图象如图所示,点
的部分图象如图所示,点 、
、 是最高点,点
是最高点,点 是最低点.若△
是最低点.若△ 是直角三角形(C为直角),则
是直角三角形(C为直角),则 的值为
的值为
A.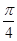 | B. | C.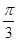 | D. |
已知函数 ,若
,若 ,则
,则 ( )
( )
A. | B. | C.2014 | D.2015 |
cos17°sin43°+sin163°sin47°
A.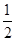 | B.一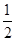 | C. | D.一 |
某扇形的半径为1cm,它的弧长为2cm,那么该扇形的圆心角为( )
| A.2° | B.4rad | C.4° | D.2rad |
为了得到函数y=cos(x+ )的图象,只需把余弦曲线y=cosx上的所有的点 ( )
)的图象,只需把余弦曲线y=cosx上的所有的点 ( )
A.向左平移 个单位长度 个单位长度 | B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 | D.向右平移 个单位长度 个单位长度 |
定义运算: ,例如
,例如 ,则
,则 的最大值为( )
的最大值为( )
| A.4 | B.3 | C.2 | D.1 |