题目内容
若函数 (
(
 ),又
),又 ,
, ,且
,且 的最小值为
的最小值为 ,则正数
,则正数 的值是( )
的值是( )
A. | B.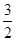 | C. | D. |
D
解析试题分析: ,又
,又 ,
, ,说明在
,说明在 时函数取得最小值,在
时函数取得最小值,在 时,函数图象与
时,函数图象与 轴的交点,即平衡点,
轴的交点,即平衡点, 的最小值应为
的最小值应为 ,即
,即 ,所以
,所以 .
.
考点:三角函数图象与性质以及引入辅助角的方法.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
将函数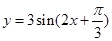 的图象向右平移
的图象向右平移 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
A.在区间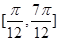 上单调递减 上单调递减 | B.在区间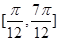 上单调递增 上单调递增 |
C.在区间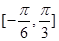 上单调递减 上单调递减 | D.在区间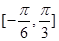 上单调递增 上单调递增 |
下面的函数中,周期为 的偶函数是( )
的偶函数是( )
A. | B. |
C. | D. |
设 ,
, ,
, ,则( )
,则( )
A. | B. | C. | D. |
半径为 ,中心角为
,中心角为 所对的弧长是( ).
所对的弧长是( ).
A. | B. | C. | D. |
函数 的图象可看成
的图象可看成 的图象按如下平移变换而得到的( ).
的图象按如下平移变换而得到的( ).
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 | C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
己知a为锐角,且 ,
, ,则sina的值是( ).
,则sina的值是( ).
A. | B. | C. | D. |
已知f(x)=asin2x+bcos2x,其中a,b∈R,ab≠0,若f(x)≤|f( )|对一切x∈R恒成立,且f(
)|对一切x∈R恒成立,且f( )>0,则f(x)的单调递增区间是( )
)>0,则f(x)的单调递增区间是( )
A.[kπ- ,kπ+ ,kπ+ ](k∈Z) ](k∈Z) | B.[kπ+ ,kπ+ ,kπ+ ](k∈Z) ](k∈Z) |
C.[kπ,kπ+ ](k∈Z) ](k∈Z) | D.[kπ- ,kπ](k∈Z) ,kπ](k∈Z) |
 (ω>0)的图象与直线y=-2的两个相邻公共点之间的距离等于π,则
(ω>0)的图象与直线y=-2的两个相邻公共点之间的距离等于π,则 的单调递减区间是( )
的单调递减区间是( )


