题目内容
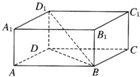 已知长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1,BD1与平面AC所成的角为,则cosθ的值是
已知长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1,BD1与平面AC所成的角为,则cosθ的值是
- A.
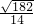
- B.
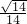
- C.
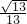
- D.
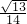
A
分析:由已知中长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1,结合正方体的几何特征,结合线面夹角的定义,我们易得∠D1BD即为BD1与平面AC所成的角,解Rt△D1BD,即可得到BD1与平面AC所成的角的余弦值.
解答:∵在长方体ABCD-A1B1C1D1中,
D1在平面AC上的射影为D,
故BD1在平面AC上的射影为BD,
则∠D1BD即为BD1与平面AC所成的角
∵AB=3,BC=2,BB1=1,
∴在Rt△D1BD中,D1D=BB1=1,BD=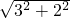 =
= ,D1B=
,D1B=
∴cosθ=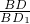 =
=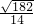
故选A
点评:本题考查的知识点是线面夹角,其中根据已知确定出∠D1BD即为BD1与平面AC所成的角,是解答本题的关键.
分析:由已知中长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1,结合正方体的几何特征,结合线面夹角的定义,我们易得∠D1BD即为BD1与平面AC所成的角,解Rt△D1BD,即可得到BD1与平面AC所成的角的余弦值.
解答:∵在长方体ABCD-A1B1C1D1中,
D1在平面AC上的射影为D,
故BD1在平面AC上的射影为BD,
则∠D1BD即为BD1与平面AC所成的角
∵AB=3,BC=2,BB1=1,
∴在Rt△D1BD中,D1D=BB1=1,BD=
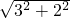 =
= ,D1B=
,D1B=
∴cosθ=
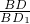 =
=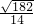
故选A
点评:本题考查的知识点是线面夹角,其中根据已知确定出∠D1BD即为BD1与平面AC所成的角,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知长方体ABCD-A1B1C1D1,下列向量的数量积一定不为0的是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点.
已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点. 已知长方体ABCD-A1B1C1D1中,DA=DD1=1,
已知长方体ABCD-A1B1C1D1中,DA=DD1=1, 已知长方体ABCD-A1B1C1D1中,M、N分别是BB1和BC的中点,AB=4,AD=2,
已知长方体ABCD-A1B1C1D1中,M、N分别是BB1和BC的中点,AB=4,AD=2, 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.