题目内容
已知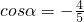 ,且α为第三象限角.
,且α为第三象限角.
(Ⅰ)求sin(π+α)的值;
(Ⅱ)分别计算tan2α,cos2α的值并判断角2α所在的象限.
解:(Ⅰ)由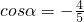 ,且α为第三象限角,
,且α为第三象限角,
可得 .
.
所以, .
.
(Ⅱ)由 ,
,
可得 .
. .
.
由tan2α>0,cos2α>0,可知角2α在第一象限.
分析:(I)利用sin2α+cos2α=1以及α为第三象限角,求出sinα,然后利用诱导公式得出sin(π+α)=-sinα,即可求出结果.
(II)由(I)求出tanα,然后利用二倍角的正切函数和余弦函数公式求出tan2α,cos2α,再根据tan2α,cos2α的正负判断出2α所在的象限.
点评:本题考查了同角三角函数的基本关系,二倍角的余弦和正切公式,解题的关键是灵活运用相关公式,同时解题的过程要注意角的位置.
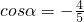 ,且α为第三象限角,
,且α为第三象限角,可得
 .
.所以,
 .
. (Ⅱ)由
 ,
,可得
 .
. .
.由tan2α>0,cos2α>0,可知角2α在第一象限.
分析:(I)利用sin2α+cos2α=1以及α为第三象限角,求出sinα,然后利用诱导公式得出sin(π+α)=-sinα,即可求出结果.
(II)由(I)求出tanα,然后利用二倍角的正切函数和余弦函数公式求出tan2α,cos2α,再根据tan2α,cos2α的正负判断出2α所在的象限.
点评:本题考查了同角三角函数的基本关系,二倍角的余弦和正切公式,解题的关键是灵活运用相关公式,同时解题的过程要注意角的位置.

练习册系列答案
相关题目
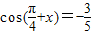 ,且x是第三象限角,则
,且x是第三象限角,则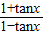 的值为( )
的值为( )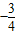
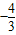


 ,且a为第三象限角,则cosa=( )
,且a为第三象限角,则cosa=( )


