题目内容
若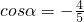 ,α是第三象限的角,则
,α是第三象限的角,则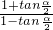 =________.
=________.
-
分析:利用平方关系及α所在的象限可求出sinα,由商数关系可得出tanα,利用正切的倍角公式可求得 ,再根据α所在的象限可判断出
,再根据α所在的象限可判断出 所在的象限,进而确定
所在的象限,进而确定 的值即可.
的值即可.
解答:∵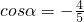 ,α是第三象限的角,∴
,α是第三象限的角,∴ =
=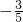 ,
,
∴ =
= .
.
∵ ,∴
,∴ ,化为,
,化为, ,解得
,解得 或-3.
或-3.
∵α是第三象限的角,∴ ,∴
,∴ (k∈Z).
(k∈Z).
①当k=2n(n∈N*)时, ,可知
,可知 是第二象限的角,则
是第二象限的角,则 ,∴
,∴ ;
;
②当k=2n+1(n∈N*)时, ,可知
,可知 是第四象限的角,则
是第四象限的角,则 ,∴
,∴ ;
;
因此 应舍去,故
应舍去,故 .
.
∴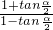 =
= =
= .
.
故答案为 .
.
点评:熟练掌握同角三角函数基本关系式、倍角公式、由α所在的象限判断 所在象限是解题的关键.
所在象限是解题的关键.

分析:利用平方关系及α所在的象限可求出sinα,由商数关系可得出tanα,利用正切的倍角公式可求得
 ,再根据α所在的象限可判断出
,再根据α所在的象限可判断出 所在的象限,进而确定
所在的象限,进而确定 的值即可.
的值即可.解答:∵
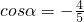 ,α是第三象限的角,∴
,α是第三象限的角,∴ =
=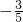 ,
,∴
 =
= .
.∵
 ,∴
,∴ ,化为,
,化为, ,解得
,解得 或-3.
或-3.∵α是第三象限的角,∴
 ,∴
,∴ (k∈Z).
(k∈Z).①当k=2n(n∈N*)时,
 ,可知
,可知 是第二象限的角,则
是第二象限的角,则 ,∴
,∴ ;
;②当k=2n+1(n∈N*)时,
 ,可知
,可知 是第四象限的角,则
是第四象限的角,则 ,∴
,∴ ;
;因此
 应舍去,故
应舍去,故 .
.∴
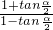 =
= =
= .
.故答案为
 .
.点评:熟练掌握同角三角函数基本关系式、倍角公式、由α所在的象限判断
 所在象限是解题的关键.
所在象限是解题的关键. 
练习册系列答案
相关题目
 ,且
,且 是第三象限的角,则
是第三象限的角,则 的值为
.
的值为
.  ,α是第三象限的角,则cos(α+
,α是第三象限的角,则cos(α+ )= .
)= . ,a是第三象限的角,则
,a是第三象限的角,则 = .
= . ,α是第三象限的角,则
,α是第三象限的角,则 =( )
=( )

 ,α是第三象限的角,则sin(α+
,α是第三象限的角,则sin(α+ )=( )
)=( )


