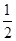题目内容
对任意的x∈R,函数f(x)=x3+ax2+7ax不存在
极值点的充要条件是( )
| A.a=0或a="7" | B.a<0或a>21 | C.0≤a≤21 | D.a=0或a=21 |
C
解析试题分析: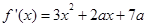 ,无极值点,则
,无极值点,则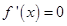 ,即
,即
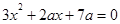 无解,
无解, ,解得
,解得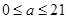 .
.
考点:极值,一元二次方程的根.

练习册系列答案
相关题目
设三次函数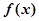 的导函数为
的导函数为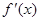 ,函数
,函数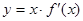 的图象的一部分如下图所示,则( )
的图象的一部分如下图所示,则( )
A.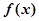 极大值为 极大值为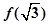 ,极小值为 ,极小值为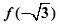 |
B.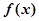 极大值为 极大值为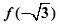 ,极小值为 ,极小值为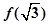 |
C.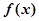 极大值为 极大值为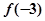 ,极小值为 ,极小值为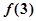 |
D.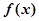 极大值为 极大值为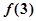 ,极小值为 ,极小值为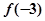 |
若曲线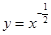 在点
在点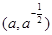 处的切线与两坐标轴围成的三角形面积为18.则
处的切线与两坐标轴围成的三角形面积为18.则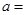 ( )
( )
| A.64 | B.32 | C.16 | D.8 |
函数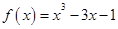 ,若对于区间[-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是( )
,若对于区间[-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是( )
| A.20 | B.18 | C.3 | D.0 |
设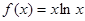 ,若
,若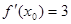 ,则
,则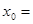 ( )
( )
A.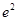 | B.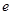 | C.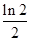 | D.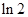 |
函数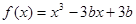 在
在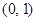 内有极小值,则
内有极小值,则
A.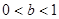 | B.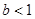 | C.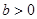 | D. |
若函数f(x)=2x2-lnx在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
| A.[1,+∞) | B.[1,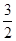 ) ) | C.[1,2) | D.[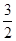 ,2) ,2) |
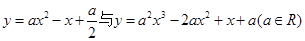 的图像不可能的是( )
的图像不可能的是( )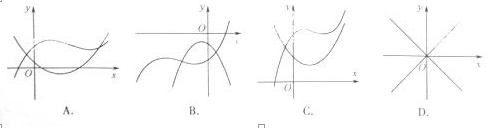
 ,g(x)=xα在点P(1,1)处的切线分别为l1,l2,且l1⊥l2,则实数α的值为( )
,g(x)=xα在点P(1,1)处的切线分别为l1,l2,且l1⊥l2,则实数α的值为( )