题目内容
 如图,A,B分别是单位圆与x轴,y轴正半轴的交点,点P为单位圆的
如图,A,B分别是单位圆与x轴,y轴正半轴的交点,点P为单位圆的 |
| AB |
(1)当
| CB |
| OP |
| π |
| 4 |
(2)若
| OP |
| OQ |
| OA |
| OA |
| OQ |
分析:(1)由题意给出点A、B、P的坐标,从而得到向量
、
的坐标,由向量平行的条件列式,结合同角三角函数的关系解出tanθ=
,再根据两角差的正切公式,即可算出tan(θ-
)的值;
(2)根据题意可得四边形OAQP是平行四边形,利用三角形面积公式、数量积的公式与三角恒等变换公式,建立关系式并化简,可得
•
+S=
sin(θ+
)+1,最后根据正弦函数的图象与性质加以计算,可得所求的最大值.
| CB |
| OP |
| 1 |
| 2 |
| θ |
| 4 |
(2)根据题意可得四边形OAQP是平行四边形,利用三角形面积公式、数量积的公式与三角恒等变换公式,建立关系式并化简,可得
| OA |
| OQ |
| 2 |
| π |
| 4 |
解答:解:(1)根据题意,可得A、B、P的坐标分别为(1,0)、(0,1)、(cosθ,sinθ),
∴
=(1,0),
=(cosθ,sinθ).
又∵C(-2,0),可得
=(2,1),
∴由
∥
,得cosθ-2sinθ=0,可得sinθ=
cosθ,
∴tanθ=
=
,
因此,tan(θ-
)=
=-
;
(2)∵
,
∴四边形OAQP是平行四边形,
可得OAQP的面积为
.
由(1)得
,
=(1,0),
∴
∴
•
+S=sinθ+cosθ+1=
sin(θ+
)+1,其中0<θ<π.
因此,当θ+
=
即θ=
时,
•
+S的最大值为
+1.
∴
| OA |
| OP |
又∵C(-2,0),可得
| CB |
∴由
| CB |
| OP |
| 1 |
| 2 |
∴tanθ=
| sinθ |
| cosθ |
| 1 |
| 2 |
因此,tan(θ-
| θ |
| 4 |
| tanθ-1 |
| tanθ+1 |
| 1 |
| 3 |
(2)∵
|
∴四边形OAQP是平行四边形,
可得OAQP的面积为
|
由(1)得
|
| OA |
∴
|
∴
| OA |
| OQ |
| 2 |
| π |
| 4 |
因此,当θ+
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| OA |
| OQ |
| 2 |
点评:本题给出单位圆中的向量,求数量积与四边形面积之和的最大值.着重考查了向量的数量积公式、三角恒等变换公式、同角三角函数的基本关系与三角函数的图象与性质等知识,属于中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
(14分)如图,A,B,C为函数![]() 的图象
的图象
|
(1)设![]() ABC的面积为S 求S=f (t) ;
ABC的面积为S 求S=f (t) ;
(2)判断函数S=f (t)的单调性;
(3) 求S=f (t)的最大值.
(14分)如图,A,B,C为函数![]() 的图象
的图象
|
(1)设![]() ABC的面积为S 求S=f (t) ;
ABC的面积为S 求S=f (t) ;
(2)判断函数S=f (t)的单调性;
(3) 求S=f (t)的最大值.
 的图象上的三点,它们的横坐标分别是t,
t+2, t+4(t
的图象上的三点,它们的横坐标分别是t,
t+2, t+4(t 1).
1).
 ABC的面积为S 求S=f (t)
;
ABC的面积为S 求S=f (t)
; 的图象
的图象 1).
1). ABC的面积为S 求S=f
(t)
ABC的面积为S 求S=f
(t) 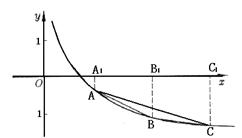
 的图象上的三点,它们的横坐标分别是t,t+2,t+4(t≥1)。
的图象上的三点,它们的横坐标分别是t,t+2,t+4(t≥1)。 

