题目内容
如图,A,B,C为函数 的图象上的三点,它们的横坐标分别是t,
t+2, t+4(t
的图象上的三点,它们的横坐标分别是t,
t+2, t+4(t 1).
1).

(1)设 ABC的面积为S 求S=f (t)
;
ABC的面积为S 求S=f (t)
;
(2)判断函数S=f (t)的单调性;
(3) 求S=f (t)的最大值.
【答案】
(1) S= 
(2) S=f (t)在  是是减函数
是是减函数
(3) 最大值是f (1) 
【解析】解:(1)过A,B,C,分别作AA1,BB1,CC1垂直于x轴,垂足为A1,B1,C1,
则S=S梯形AA1B1B+S梯形BB1C1C-S梯形AA1C1C.

(2)因为v= 在
在 上是增函数,且v
上是增函数,且v 5,
5,
 上是减函数,且1<u
上是减函数,且1<u
 ; S
; S 上是增函数,
上是增函数,
所以复合函数S=f(t)  上是减函数
上是减函数
(3)由(2)知t=1时,S有最大值,最大值是f (1) 

练习册系列答案
相关题目
 上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )
上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )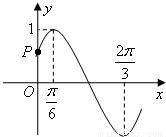



 上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )
上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )



 满足
满足 ,
, 为
为 的图象如图所示,若两个正数
的图象如图所示,若两个正数 满足
满足 ,则
,则 的取值范围是
的取值范围是 B、
B、
 D、
D、

 上的函数
上的函数 满足
满足 ,
, 为
为 的图像如图所示,若两个正数
的图像如图所示,若两个正数 、
、 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C.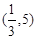 D.
D.

 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.