题目内容
已知定义在 上的函数
上的函数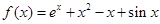 ,则曲线
,则曲线 在点
在点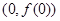 处的切线方程是( )
处的切线方程是( )
A. | B.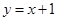 | C.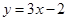 | D.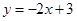 |
B.
解析试题分析: 又
又 由点斜式可得曲线
由点斜式可得曲线 在点
在点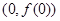 处的切线方程为
处的切线方程为 .
.
考点:导数的几何意义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
直线y=2x与抛物线y=3-x2所围成的阴影部分的面积( )
A.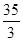 | B.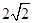 | C.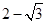 | D.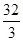 |
已知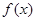 为定义在
为定义在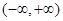 上的可导函数,
上的可导函数,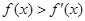 对于
对于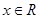 恒成立,且
恒成立,且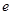 为自然对数的底数,则( )
为自然对数的底数,则( )
A.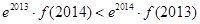 |
B.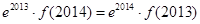 |
C.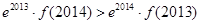 |
D.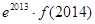 与 与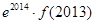 的大小不能确定 的大小不能确定 |
设函数 ,若
,若 ,则
,则 ( )
( )
A. | B. | C. | D.2 |
 在区间
在区间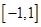 上的最大值是( )
上的最大值是( )
| A.-2 | B.0 | C.2 | D.4 |
由直线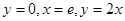 及曲线
及曲线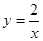 所围成的封闭的图形的面积为( )
所围成的封闭的图形的面积为( )
A.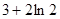 | B.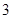 | C.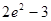 | D. |
若存在过点(1,0)的直线与曲线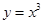 和
和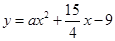 都相切,则
都相切,则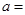 ( )
( )
A.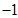 或 或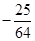 | B.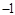 或 或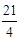 | C.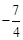 或 或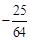 | D.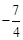 或 或 |
定义方程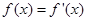 的实数根
的实数根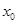 叫做函数
叫做函数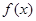 的“新驻点”,若函数
的“新驻点”,若函数
 的“新驻点”分别为
的“新驻点”分别为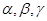 ,则
,则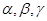 的大小关系为( )
的大小关系为( )
A.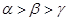 | B.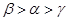 | C.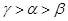 | D.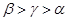 |
定义在 上的函数
上的函数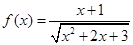 ,则
,则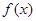 ( )
( )
| A.既有最大值也有最小值 | B.既没有最大值,也没有最小值 |
| C.有最大值,但没有最小值 | D.没有最大值,但有最小值 |