题目内容
 在区间
在区间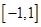 上的最大值是( )
上的最大值是( )
| A.-2 | B.0 | C.2 | D.4 |
C
解析试题分析: ,所以
,所以 ,由于
,由于 ,解得
,解得 ,当
,当 时,
时, ,当
,当 时,
时, ,故函数
,故函数 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,故函数
上单调递减,故函数 在
在 处取得极大值,亦即最大值,即
处取得极大值,亦即最大值,即 ,故选C.
,故选C.
考点:利用导数求函数的最值

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
定义在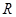 上的函数
上的函数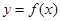 ,满足
,满足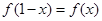 ,
,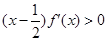 ,若
,若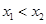 且
且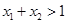 ,则有( )
,则有( )
A.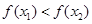 | B.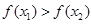 | C.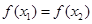 | D.不能确定 |
已知函数 满足
满足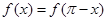 ,且当
,且当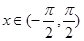 时,
时,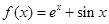 ,则( )
,则( )
A.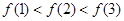 | B.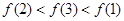 |
C. | D.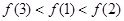 |
设函数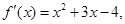 则
则 的单调减区间( )
的单调减区间( )
A.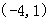 | B.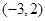 | C. | D.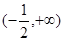 |
已知曲线方程 ,若对任意实数
,若对任意实数 ,直线
,直线 都不是曲线
都不是曲线 )的切线,则
)的切线,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. 且 且 |
已知定义在 上的函数
上的函数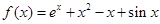 ,则曲线
,则曲线 在点
在点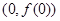 处的切线方程是( )
处的切线方程是( )
A. | B.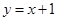 | C.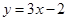 | D.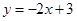 |
已知R上可导函数 的图像如图所示,则不等式
的图像如图所示,则不等式 的解集为( )
的解集为( )
A. |
B. |
C. |
D. |
已知点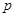 在曲线
在曲线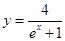 上,
上,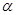 为曲线在点
为曲线在点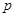 处的切线的倾斜角,则
处的切线的倾斜角,则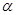 的取值范围是( )
的取值范围是( )
A.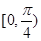 | B.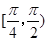 | C.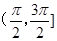 | D.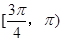 |
若过点 的直线与曲线
的直线与曲线 和
和 都相切,则
都相切,则 的值为 ( )
的值为 ( )
| A.2 | B. | C.2或 | D.3或 |