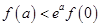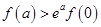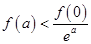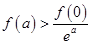题目内容
已知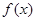 为定义在
为定义在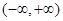 上的可导函数,
上的可导函数,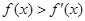 对于
对于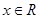 恒成立,且
恒成立,且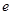 为自然对数的底数,则( )
为自然对数的底数,则( )
A.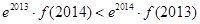 |
B.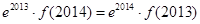 |
C.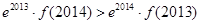 |
D.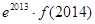 与 与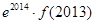 的大小不能确定 的大小不能确定 |
A
解析试题分析:函数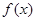 为定义在
为定义在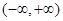 上的可导函数,满足
上的可导函数,满足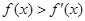 ,则函数为指数函数,可设函数
,则函数为指数函数,可设函数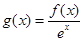 ,则导函数
,则导函数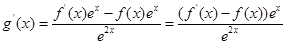 ,因为
,因为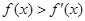 ,所以
,所以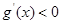 ,
,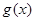 在
在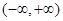 上为减函数,
上为减函数,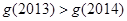 ,即
,即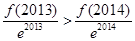 ,从而得
,从而得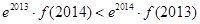 .
.
考点:函数与导数运算法则、利用导数研究函数的单调性.

练习册系列答案
相关题目
若曲线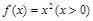 在点
在点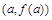 处的切线与两条坐标轴围成的三角形的面积为54,则
处的切线与两条坐标轴围成的三角形的面积为54,则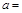 ( )
( )
| A.3 | B.6 | C.9 | D.18 |
曲线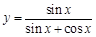 在点
在点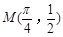 处的切线的斜率为
处的切线的斜率为
A.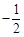 | B.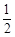 | C. | D.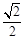 |
已知函数 满足
满足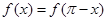 ,且当
,且当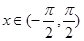 时,
时,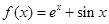 ,则( )
,则( )
A.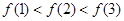 | B.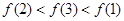 |
C. | D.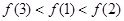 |
已知函数 的导函数为
的导函数为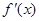 ,且满足
,且满足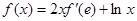 ,则
,则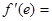 ( )
( )
A.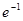 | B. | C. | D.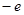 |
设函数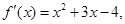 则
则 的单调减区间( )
的单调减区间( )
A.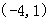 | B.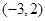 | C. | D.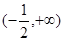 |
已知定义在 上的函数
上的函数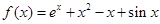 ,则曲线
,则曲线 在点
在点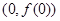 处的切线方程是( )
处的切线方程是( )
A. | B.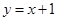 | C.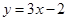 | D.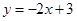 |
曲线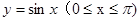 与直线y=
与直线y=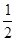 围成的封闭图形的面积为( )
围成的封闭图形的面积为( )
A.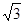 | B.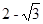 | C. | D.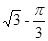 |
 是定义在R上的可导函数,且满足
是定义在R上的可导函数,且满足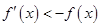 ,对于任意的正数
,对于任意的正数 ,下面不等式恒成立的是( )
,下面不等式恒成立的是( )