题目内容
【题目】已知椭圆![]() ,过
,过![]() 的焦点且垂直于
的焦点且垂直于![]() 轴的直线被
轴的直线被![]() 截得的弦长为
截得的弦长为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过右焦点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴相交于点
轴相交于点![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)根据通径可求过![]() 的焦点且垂直于
的焦点且垂直于![]() 轴的直线被
轴的直线被![]() 截得的弦长为
截得的弦长为![]() ,再由椭圆
,再由椭圆![]() 的离心率为
的离心率为![]() 及椭圆解得a、b,可得椭圆方程;
及椭圆解得a、b,可得椭圆方程;
(2)依题意,得直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,与椭圆联立利用韦达定理可得线段
,与椭圆联立利用韦达定理可得线段![]() 的中点为
的中点为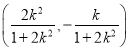 ,可得线段
,可得线段![]() 的垂直平分线的方程为
的垂直平分线的方程为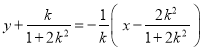 ,代入
,代入![]() 解得
解得![]() 或
或![]() ,由此得出直线
,由此得出直线![]() 的方程.
的方程.
(1)过![]() 的焦点且垂直于
的焦点且垂直于![]() 轴的直线被
轴的直线被![]() 截得的弦长为
截得的弦长为![]() ,
,
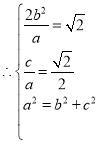 ,解得
,解得![]() ,
,![]() .
.
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)依题意,得直线![]() 的斜率存在且不为0,
的斜率存在且不为0,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
由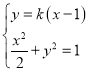 ,得
,得![]() .
.
可得![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() 线段
线段![]() 的中点为
的中点为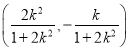 .
.
线段![]() 的垂直平分线的方程为
的垂直平分线的方程为
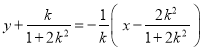 .
.
令![]() ,得
,得![]() .
.
![]() ,解得
,解得![]() 或
或![]() .
.
![]() 直线
直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若
,若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为![]() ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为![]() .
.
(Ⅰ)已知函数![]() ,若
,若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)已知![]() ,
,![]() 且
且![]() 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
求证:![]() ;
;
(Ⅲ)定义集合![]()
请问:是否存在常数![]() ,使得
,使得![]() ,
,![]() ,有
,有![]() 成立?若存在,求出
成立?若存在,求出![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.