题目内容
已知椭圆 的焦点为
的焦点为 ,
, ,在长轴
,在长轴 上任取一点
上任取一点 ,过
,过 作垂直于
作垂直于 的直线交椭圆于点
的直线交椭圆于点 ,则使得
,则使得 的点
的点 的概率为( )
的概率为( )
A. | B. | C. | D. |
D
解析试题分析:设 ,则
,则
 ,
, ,概率为
,概率为 ,选D
,选D
考点:本题考查了几何概率的求法
点评:求几何概率的基本题型有:长度问题、角度问题、面积问题、体积问题与及生活中实际问题(如时间)等等.

练习册系列答案
相关题目
抛物线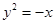 的焦点坐标为( )
的焦点坐标为( )
A.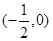 | B.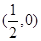 | C.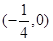 | D.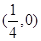 |
过双曲线的一个焦点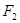 作垂直于实轴的弦
作垂直于实轴的弦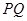 ,
,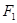 是另一焦点,若∠
是另一焦点,若∠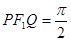 ,则双曲线的离心率
,则双曲线的离心率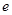 等于( )
等于( )
A. | B.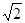 | C.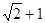 | D.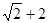 |
以抛物线 的焦点为圆心,且过坐标原点的圆的方程为( )
的焦点为圆心,且过坐标原点的圆的方程为( )
A. | B. |
C. | D. |
在抛物线 上,横坐标为
上,横坐标为 的点到焦点的距离为
的点到焦点的距离为 ,则
,则 的值为( )
的值为( )
| A.0.5 | B.1 | C.2 | D.4 |
方程 表示焦点在
表示焦点在 轴的双曲线,则
轴的双曲线,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
 为双曲线
为双曲线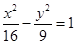 的左焦点,在
的左焦点,在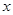 轴上
轴上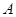 ,以
,以 为直径的圆与双曲线左、右两支在
为直径的圆与双曲线左、右两支在 、
、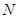 ,则
,则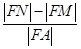 的值为( )
的值为( )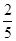
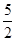
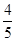
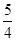
 和
和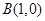 ,动点
,动点 在直线
在直线 上移动,椭圆
上移动,椭圆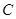 以
以 为焦点且经过点
为焦点且经过点 ,记椭圆
,记椭圆 ,则函数
,则函数 的大致图像是( )
的大致图像是( )
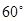 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( ) B.
B.  C.
C.  D.
D. 