题目内容
15.要从高二年级六个班中选出10人组成篮球队,每班至少要选出1个参加,则分配名额的方案有多少种?分析 由题意知可以可以先分给6个班每班一个名额,剩下的4个名额有五种分配方案,(1,1,1,1),(2,1,1),(2,2),(3,1),(4)根据分类计数原理得到结果.
解答 解:由题意知可以先分给6个班每班一个名额,
剩下的4个名额有四种分配方案,(1,1,1,1),(2,1,1),(2,2),(3,1),(4)
第一类(1,1,1,1),从6个班中选4个班,一班一个,共有C64=15种,
第二类(2,1,1),从6个班中选1个班,分2个,再选2个班,一班一个,共有C61C52=60种,
第三类(2,2),从6个班中选2个班,一班二个,共有C62=15种,
第四类(3,1),从6个班中选2个班,一班一个,一班三个,共有C61C51=30种,
第五类(4),从6个班中选1个班,有6种,
根据分类计数原理可得15+60+15+30+6=126.
点评 本题考查分类计数原理,对于复杂一点的计数问题,有时分类以后,每类方法并不都是一步完成的,必须在分类后又分步,综合利用两个原理解决,即类中有步,步中有类.

练习册系列答案
相关题目
20.执行下面的程序框图,则输出的n的值为( )
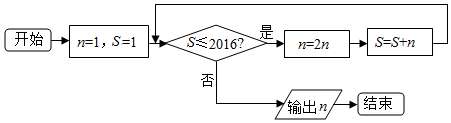

| A. | 10 | B. | 11 | C. | 1024 | D. | 2048 |
6.若sinx-2cosx=$\sqrt{5}$,则tanx=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |