题目内容
13.f(x)=ax2-c,且-4≤f(1)≤-1,-1≤f(2)≤5,则f(3)的取值范围[-1,20].分析 法一、由已知求出a-c,4a-c的范围,把f(3)转化为a-c,4a-c的形式得答案.
法二、由-4≤a-c≤-1,-1≤4a-c≤5作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.
解答 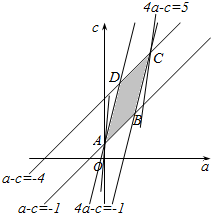 解:法一、∵f(x)=ax2-c,且-4≤f(1)≤-1,-1≤f(2)≤5,
解:法一、∵f(x)=ax2-c,且-4≤f(1)≤-1,-1≤f(2)≤5,
∴-4≤a-c≤-1,-1≤4a-c≤5,
则f(3)=9a-c=m(a-c)+n(4a-c)=(m+4n)a-(m+n)c,
∴$\left\{\begin{array}{l}{m+4n=9}\\{m+n=1}\end{array}\right.$,解得m=-$\frac{5}{3}$,n=$\frac{8}{3}$.
∴$\frac{5}{3}≤-\frac{5}{3}(a-c)≤\frac{20}{3}$,$-\frac{8}{3}≤\frac{8}{3}(4a-c)≤\frac{40}{3}$.
∴f(3)=9a-c=$-\frac{5}{3}(a-c)+\frac{8}{3}(4a-c)∈$[-1,20].
法二、
由-4≤a-c≤-1,-1≤4a-c≤5作出可行域如图,
联立$\left\{\begin{array}{l}{a-c=-4}\\{4a-c=5}\end{array}\right.$,解得C(3,7),
化目标函数z=f(3)=9a-c为c=9a-z,
由图可知,当直线c=9a-z过A(0,1)时z有最小值-1;
当直线c=9a-z过C(3,7)时z有最大值为20.
故答案为:[-1,20].
点评 本题考查简单的线性规划,考查利用待定系数法求解不等式的范围问题,是中档题.

练习册系列答案
相关题目
4.等差数列{an}中,a1+a3+a5=π,则cosa3=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
18.已知i是虚数单位,复数$\overline{Z}$=|1-$\sqrt{3}$i|($\sqrt{3}$-i),$\overline{Z}$是Z的共轭复数,则Z的虚部为( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
2.在数列{an}中,a1=1,a2=$\frac{1}{4}$,若{$\frac{1}{{a}_{n}}$}等差数列,则数列{an}的第10项为( )
| A. | $\frac{1}{22}$ | B. | $\frac{1}{25}$ | C. | $\frac{1}{28}$ | D. | $\frac{1}{31}$ |