题目内容
9.已知f1(x)=|x-1|,fn+1(x)=|(n+1)fn(x)-1|,n∈N*,若函数y=f3(x)-kx恰有4个不同零点,则正实数k的值为2.分析 由题意化简f3(x)=|3f2(x)-1|=$\left\{\begin{array}{l}{|6x-10|,x≥\frac{3}{2}}\\{|6x-8|,1≤x<\frac{3}{2}}\\{|6x-4|,\frac{1}{2}≤x<1}\\{|6x-2|,x<\frac{1}{2}}\end{array}\right.$;从而作函数y=f3(x)与函数y=kx的图象,结合函数图象求解即可.
解答 解:∵f1(x)=|x-1|,
∴f2(x)=|2f1(x)-1|
=$\left\{\begin{array}{l}{|2x-3|,x≥1}\\{|1-2x|,x<1}\end{array}\right.$,
∴f3(x)=|3f2(x)-1|
=$\left\{\begin{array}{l}{|6x-10|,x≥\frac{3}{2}}\\{|6x-8|,1≤x<\frac{3}{2}}\\{|6x-4|,\frac{1}{2}≤x<1}\\{|6x-2|,x<\frac{1}{2}}\end{array}\right.$;
作函数y=f3(x)与函数y=kx的图象如下,
结合图象可得,
当函数y=f3(x)-kx恰有4个不同零点时,
y=kx过点(1,2);
故k=2;
故答案为:2.
点评 本题考查了数形结合的图象应用及绝对值函数的化简与应用,属于中档题.

练习册系列答案
相关题目
14.设函数f(x)=x|x|+bx+c,有下列四个结论:
①方程f(x)=0至少有一个实数根;
②方程f(x)=0至多有两个实数根;
③函数f(x)的图象关于点(0,c)对称;
④当b≥0时,f(x)在R上是增函数.
其中正确的结论是( )
①方程f(x)=0至少有一个实数根;
②方程f(x)=0至多有两个实数根;
③函数f(x)的图象关于点(0,c)对称;
④当b≥0时,f(x)在R上是增函数.
其中正确的结论是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①③④ |
19.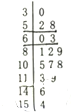 空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:
甲市2015年2月份中有15对空气质量指数PM2.5进行监测,获得PM2.5日均浓度数据茎叶图如图所示.
(Ⅰ)在15天内任取2天,求甲市空气质量类别均为良的概率;
(Ⅱ)在15天内任取2天,记甲市空气质量级别不超过三级的天数为X,求随机变量X的分布列及数学期望.
 空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
(Ⅰ)在15天内任取2天,求甲市空气质量类别均为良的概率;
(Ⅱ)在15天内任取2天,记甲市空气质量级别不超过三级的天数为X,求随机变量X的分布列及数学期望.
 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点(0,-1),且离心率为$\frac{{\sqrt{3}}}{2}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点(0,-1),且离心率为$\frac{{\sqrt{3}}}{2}$. 某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100].规定90分及其以上为合格.
某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100].规定90分及其以上为合格.