题目内容
19. 空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
(Ⅰ)在15天内任取2天,求甲市空气质量类别均为良的概率;
(Ⅱ)在15天内任取2天,记甲市空气质量级别不超过三级的天数为X,求随机变量X的分布列及数学期望.
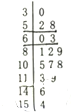
分析 (I)由茎叶图可知:甲市在15天内有4天的空气质量类别为良,利用相互独立事件的概率计算公式即可得出甲市空气质量类别均为良的概率;
(Ⅱ)利用超几何分布即可得到分布列,再利用数学期望的计算公式即可得出.
解答 解:(Ⅰ)由茎叶图知,甲市在15天内有4天的空气质量类别为良,所以P=$\frac{{C}_{4}^{2}}{{C}_{15}^{2}}$=$\frac{2}{35}$;
(Ⅱ)由茎叶图知,甲市在15天内有12天的空气质量级别不超过三级,X的可能取值为0,1,2,
则P(X=0)=$\frac{{C}_{3}^{2}}{{C}_{15}^{2}}$=$\frac{1}{35}$,P(X=1)=$\frac{{C}_{12}^{1}{C}_{3}^{1}}{{C}_{15}^{2}}$=$\frac{12}{35}$,P(X=2)=$\frac{{C}_{12}^{2}}{{C}_{15}^{2}}$=$\frac{22}{35}$.
所以X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{35}$ | $\frac{12}{35}$ | $\frac{22}{35}$ |
点评 正确理解茎叶图、相互独立事件的概率计算公式、超几何分布、随机变量的分布列、数学期望的计算公式、排列与组合的计算公式是解题的关键.

练习册系列答案
相关题目
7.(理)已知圆心为O,半径为1的圆上有不同的三个点A、B、C,其中$\overrightarrow{OA}•\overrightarrow{OB}=0$,存在实数λ,μ满足$\overrightarrow{OC}+λ\overrightarrow{OA}+u\overrightarrow{OB}=\overrightarrow 0$,则实数λ,μ的关系为( )
| A. | λ2+μ2=1 | B. | $\frac{1}{λ}+\frac{1}{μ}=1$ | C. | λμ=1 | D. | λ+μ=1 |
8.如图,在△ABC中,$\overrightarrow{AD}=\frac{2}{3}\overrightarrow{AC}$,$\overrightarrow{BP}=\frac{1}{3}\overrightarrow{BD}$,若$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$,则λ+μ的值为( )

| A. | $\frac{8}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
9.已知△ABC的三个顶点A,B,C及平面内一点P满足$\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{PC}$,则下列说法中正确的是( )
| A. | P在△ABC的内部 | B. | P在△ABC的边AB上 | ||
| C. | P在AB边所在的直线上 | D. | P在△ABC的外部 |
 如图所示的多面体 ABC-EFGH中,AB∥EG,AC∥EH,且△ABC与△EGH相似,AE⊥平面EFGH,EF=FG=$\sqrt{2},GH=1,EH=\sqrt{5},∠EGH={90°}$,且 AC=$\frac{1}{2}$EH,AE=EG
如图所示的多面体 ABC-EFGH中,AB∥EG,AC∥EH,且△ABC与△EGH相似,AE⊥平面EFGH,EF=FG=$\sqrt{2},GH=1,EH=\sqrt{5},∠EGH={90°}$,且 AC=$\frac{1}{2}$EH,AE=EG