题目内容
10．设x、y满足$\left\{\begin{array}{l}{x-y≥0}\\{x+y-2≥0}\\{x≤3}\end{array}\right.$，则目标函数z=3x-2y的最小值为1．分析 由题意作出其平面区域，将z=3x-2y化为y=$\frac{3}{2}$x-$\frac{1}{2}$z，-$\frac{1}{2}$z相当于直线y=$\frac{3}{2}$x-$\frac{1}{2}$z的纵截距，由几何意义可得．
解答 解：由题意作出其平面区域，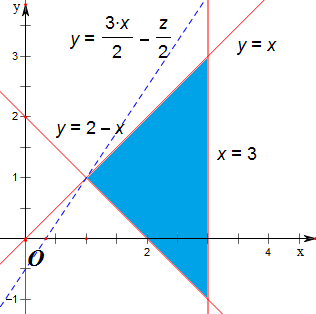
将z=3x-2y化为y=$\frac{3}{2}$x-$\frac{1}{2}$z，-$\frac{1}{2}$z相当于直线y=$\frac{3}{2}$x-$\frac{1}{2}$z的纵截距，
故求目标函数z=3x-2y的最小值，
即求直线y=$\frac{3}{2}$x-$\frac{1}{2}$z的纵截距的最大值，
由$\left\{\begin{array}{l}{y=x}\\{y=2-x}\end{array}\right.$解得，x=y=1；
故目标函数z=3x-2y的最小值为3-2=1；
故答案为：1．
点评 本题考查了简单线性规划，作图要细致认真，属于中档题．
练习册系列答案
相关题目
中，
边上的中线
长为3，且
．
的值；
边的长．
5．已知点A是半径为1的⊙O外一点，且AO=2，若M，N是⊙O一条直径的两个端点，则$\overrightarrow{AM}$$•\overrightarrow{AN}$=（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
15．实数x，y满足不等式组$\left\{\begin{array}{l}{x≥0}\\{x+2y-3≥0}\\{2x+y-3≤0}\end{array}\right.$，则下列点中不能使u=2x+y取得最大值的是（ ）
| A． | （1，1） | B． | （0，3） | C． | （$\frac{1}{2}$，2） | D． | （$\frac{3}{2}$，0） |
如图，在平面直角坐标系xOy中，点A（8，-4），P（2，t）（t＜0）在抛物线y2=2px（p＞0）上．
19．设复数z1=1+i，z2=x+2i（x∈R），若z1z2为纯虚数，则x=（ ）
| A． | 2 | B． | -2 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
20．某高中校共有学生1000名，各年级男女学生人数如下表，已知在全校学生中随机抽取1名，抽到高二男生的概率是0.16．
现用分层抽样的方法，在全校抽取40名学生，则应在高三年级抽取的学生人数为15．
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 162 | 140 | Y |
| 男生 | 163 | X | 184 |