证明极限$\underset{lim}{}$$\frac{xy}{{x}^{2}+{y}^{2}}$不存在．题目和参考答案——青夏教育精英家教网—

题目内容

2．证明极限$\underset{lim}{（x，y）→（0，0）}$$\frac{xy}{{x}^{2}+{y}^{2}}$不存在．

分析利用转换思想将原式转换成sinθcosθ，通过观察可知极限随着θ的改变而改变，因此极限不存在．

解答证明：令x=rcosθ，y=rsinθ，
则，$\frac{xy}{{x}^{2}+{y}^{2}}$=sinθcosθ，
∴它的极限随着θ改变而改变，
∴它的极限不存在

点评本题主要考察极限存在的证明，利用一步转化，可得到结论，属于基础题．

练习册系列答案

13．已知函数f（x）=|$\frac{e}{x}$-lnx|，g（x）=|e^1-x+lnx+a|
（1）将f（x）写成分段函数的形式（不用说明理由），并求f（x）的单调区间．
（2）若x≥1且-1-e^1-x＜a＜-1，比较f（x）与g（x）的大小．

10．执行如图的程序框图，则输出的i=4．

17．已知曲线y=f（x）=$\frac{1}{x}$．
（1）求曲线在点P（1，1）处的切线方程；
（2）求曲线过点Q（1，0）的切线方程；
（3）求满足斜率为-$\frac{1}{2}$的曲线的切线方程．

7．

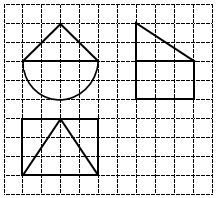如图，网格纸上的小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积是（　　）

14．已知函数f（x）=$\frac{{x}^{2}}{x-1}$对于任意的x₁，x₂，x₃∈[2，2+m]，恒有f（x₁）+f（x₂）≥f（x₃），则m的取值范围是0＜m$≤2\sqrt{2}+2$．

11．已知函数f（x）=x²+ax+b，g（x）=2x²+2，存在实数b，使得对任意x∈R，有-g（x）≤f（x）≤g（x）．
（Ⅰ）求a的取值范围；
（Ⅱ）若方程f（x）-x=0有两个实数根x₁，x₂，求|x₁-x₂|的最大值．

12．

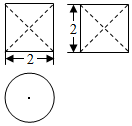如图为一个圆柱中挖去两个完全相同的圆锥而形成的几何体的三视图，则该几何体的体积为（　　）

试题分类