题目内容
 (1)如图,设圆O:x2+y2=a2的两条互相垂直的直径为AB、CD,E在弧BD上,AE交CD于K,CE交AB于L,求证:(
(1)如图,设圆O:x2+y2=a2的两条互相垂直的直径为AB、CD,E在弧BD上,AE交CD于K,CE交AB于L,求证:(| EK |
| AK |
| EL |
| CL |
(2)将椭圆
| x2 |
| a2 |
| y2 |
| b2 |
(3)如图,若AB、CD是过椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
| EK |
| AK |
| EL |
| CL |
分析:(1)如图所示,过点E作EF⊥AB,垂足为F点.由于CD⊥AB,可得EF∥CD,利用平行线的性质可得
=
,
=
,再利用EF2+FO2=OE2=a2,即可证明为定值.
(2)命题:如图,设椭圆
+
=1(a>b>0),椭圆的长轴、短轴分别为AB、CD,E在椭圆的BD部分上,AE交CD于K,CE交AB于L,求证:(
)2+(
)2为定值.与(1)类比:再利用点E满足椭圆的方程即可证明为定值.
(3)如图所示,过点E分别作EF∥CD交AB与点F,EM∥AB交直线CD于点M.
可得
=
,
=
.设A(x1,y1),C(x2,y2),D(-x2,-y2),B(-x1,-y1).E(x0,y0).
则
+
=1.设直线AB的方程为y=kx(k≠0),则直线CD的方程为y=-
x.直线EF的方程为y-y0=-
(x-x0),直线EM的方程为y-y0=k(x-x0).
联立方程可解得xF.xM.
,
.可得(
)2=(
)2=
=
.同理(
)2=
.
于是(
)2+(
)2=
+
=
,代入计算即可.
| EK |
| AK |
| FO |
| OA |
| EL |
| CL |
| EF |
| CO |
(2)命题:如图,设椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| EK |
| AK |
| EL |
| CL |
(3)如图所示,过点E分别作EF∥CD交AB与点F,EM∥AB交直线CD于点M.
可得
| EK |
| KA |
| FO |
| AO |
| EL |
| CL |
| MO |
| CO |
则
| ||
| a2 |
| ||
| b2 |
| b2 |
| a2k |
| b2 |
| a2k |
联立方程可解得xF.xM.
| x | 2 1 |
| x | 2 2 |
| EK |
| AK |
| FO |
| AO |
| ||||
x12+
|
| ||
|
| EL |
| CL |
| ||
|
于是(
| EK |
| AK |
| EL |
| CL |
| ||
|
| ||
|
| ||||||||
|
解答:解:(1)如图所示,过点E作EF⊥AB,垂足为F点,
∵CD⊥AB,∴EF∥CD,
∴
=
,
=
,
又EF2+FO2=OE2=a2,
∴(
)2+(
)2=(
)2+(
)2=
=
=1.为定值.
(2)如图,设椭圆
+
=1(a>b>0),椭圆的长轴、短轴分别为AB、CD,E在椭圆的BD部分上,AE交CD于K,CE交AB于L,求证:(
)2+(
)2为定值.
证明:过点E作EF⊥AB,垂足为F点,
∵CD⊥AB,∴EF∥CD,
∴
=
,
=
,
∴(
)2+(
)2=(
)2+(
)2=
+
=1.为定值.
(3)如图所示,
过点E分别作EF∥CD交AB与点F,EM∥AB交直线CD于点M.
∴
=
,
=
.
设A(x1,y1),C(x2,y2),D(-x2,-y2),B(-x1,-y1).E(x0,y0).
则
+
=1.
设直线AB的方程为y=kx(k≠0),则直线CD的方程为y=-
x.
直线EF的方程为y-y0=-
(x-x0),直线EM的方程为y-y0=k(x-x0).
联立
解得xF=
.
联立
,解得xM=
.
联立
解得
=
.
联立
,解得
=
.
∴(
)2=(
)2=
=
.
同理(
)2=
.
∴(
)2+(
)2=
+
=
=
=
+
=1.为定值.

∵CD⊥AB,∴EF∥CD,
∴
| EK |
| AK |
| FO |
| OA |
| EL |
| CL |
| EF |
| CO |
又EF2+FO2=OE2=a2,
∴(
| EK |
| AK |
| EL |
| CL |
| FO |
| OA |
| EF |
| CO |
| FO2+EF2 |
| a2 |
| a2 |
| a2 |
(2)如图,设椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| EK |
| AK |
| EL |
| CL |
证明:过点E作EF⊥AB,垂足为F点,

∵CD⊥AB,∴EF∥CD,
∴
| EK |
| AK |
| FO |
| OA |
| EL |
| CL |
| EF |
| CO |
∴(
| EK |
| AK |
| EL |
| CL |
| FO |
| OA |
| EF |
| CO |
| FO2 |
| a2 |
| EF2 |
| b2 |
(3)如图所示,
过点E分别作EF∥CD交AB与点F,EM∥AB交直线CD于点M.
∴
| EK |
| KA |
| FO |
| AO |
| EL |
| CL |
| MO |
| CO |
设A(x1,y1),C(x2,y2),D(-x2,-y2),B(-x1,-y1).E(x0,y0).
则
| ||
| a2 |
| ||
| b2 |
设直线AB的方程为y=kx(k≠0),则直线CD的方程为y=-
| b2 |
| a2k |
直线EF的方程为y-y0=-
| b2 |
| a2k |
联立
|
| a2ky0+b2x0 |
| a2k2+b2 |
联立
|
| a2k(kx0-y0) |
| a2k2+b2 |
联立
|
| x | 2 1 |
| a2b2 |
| a2k2+b2 |
联立
|
| x | 2 2 |
| a4k2 |
| a2k2+b2 |
∴(
| EK |
| AK |
| FO |
| AO |
| ||||
x12+
|
| ||
|
同理(
| EL |
| CL |
| ||
|
∴(
| EK |
| AK |
| EL |
| CL |
| ||
|
| ||
|
| ||||||||
|
(
| ||||||||
|
| ||
| a2 |
| ||
| b2 |
点评:熟练掌握椭圆的标准方程及其性质、平行线分线段成比例定理、直线与直线相交问题、直线与椭圆相交问题、问题转化方法等是解题的关键.本题同时考查了较强的计算能力、类比推理能力.

练习册系列答案
相关题目
 如图,设圆(x-5)2+y2=16的圆心为C,此圆和抛物线y2=px(p>0)有四个交点,若在x轴上方的两个交点为A(x1,
如图,设圆(x-5)2+y2=16的圆心为C,此圆和抛物线y2=px(p>0)有四个交点,若在x轴上方的两个交点为A(x1,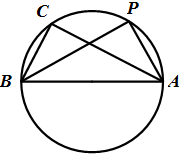 (2012•韶关二模)在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且
(2012•韶关二模)在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且
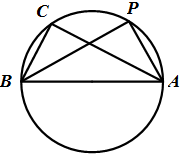 在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且
在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且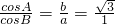 .
. 上,求△PAC面积最大值.
上,求△PAC面积最大值. .
. 上,求△PAC面积最大值.
上,求△PAC面积最大值.