题目内容
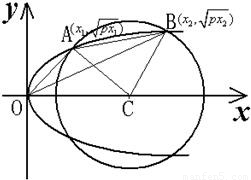
 如图,设圆(x-5)2+y2=16的圆心为C,此圆和抛物线y2=px(p>0)有四个交点,若在x轴上方的两个交点为A(x1,
如图,设圆(x-5)2+y2=16的圆心为C,此圆和抛物线y2=px(p>0)有四个交点,若在x轴上方的两个交点为A(x1,| px1 |
| px2 |
(1)求p的取值范围;
(2)求S关于p的函数f(p)的表达式及S的最大值;
(3)求当S取最大值时,向量
| CA |
| CB |
分析:(1)因为圆和抛物线有四个交点,所以联立两个方程,消去y,根据圆和抛物线的对称性,得到的关于x的一元二次方程有两个不同正根,据此可求出参数p的范围.
(2)△AOB的面积可用
|AB|乘以O到AB的距离来计算,用弦长公式计算|AB|,点到直线的距离公式计算O到AB的距离,就可得到S关于p的函数f(p)的表达式,再根据(1)中所求p的范围求最大值.
(3)用数量级的夹角公式计算即可.
(2)△AOB的面积可用
| 1 |
| 2 |
(3)用数量级的夹角公式计算即可.
解答:解:(1)把 y2=px代入(x-5)2+y2=16得 x2+(p-10)x+9=0
依题意得方程x2+(p-10)x+9=0有两个不同的正根为x1,x2
∴x1+x2=10-p,x1x2=9,∴
解得p<4又∵p>0
∴p的取值范围是(0,4)
(2)∵直线AB的斜率kAB=
=
∴AB的方程:y-
=
(x-x1),
即
x-(
+
)y+
=0,即
•x-
•y+3
=0
∴点O到AB的距离d=
,
又|AB|=
=
∴S=f(p)=
=
≤3,
当且仅当p=2时S取最大值为3
(3)S取最大值时,p=2,解方程x2-8x+9=0,得A(4-
,
-1),B(4+
,
+1)
=(-
-1,
-1),
=((
-1,
+1),
•
=-6+6=0
∴向量
,
的夹角的大小为90°.
依题意得方程x2+(p-10)x+9=0有两个不同的正根为x1,x2
∴x1+x2=10-p,x1x2=9,∴
|
∴p的取值范围是(0,4)
(2)∵直线AB的斜率kAB=
| ||||
| x1-x2 |
| ||||
|
∴AB的方程:y-
| px1 |
| ||||
|
即
| p |
| x1 |
| x2 |
| px1x2 |
| p |
| 16-p |
| p |
∴点O到AB的距离d=
3
| ||
| 4 |
又|AB|=
(x1-x2)2+p•(
|
| 64-16p |
∴S=f(p)=
| 1 |
| 2 |
| 64-16p |
3
| ||
| 4 |
| 1 |
| 2 |
| 3 | p(4-p) |
当且仅当p=2时S取最大值为3
(3)S取最大值时,p=2,解方程x2-8x+9=0,得A(4-
| 7 |
| 7 |
| 7 |
| 7 |
| CA |
| 7 |
| 7 |
| CB |
| 7 |
| 7 |
| CA |
| CB |
∴向量
| CA |
| CB |
点评:本题考查了圆与双曲线位置关系的判断,以及弦长公式,点到直线距离公式,向量的数量积公式的应用,用到公式较多,平时做题中应注意积累.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤. (考生注意:只能从下列A、B、C三题中选做一题,如果多做,则按第一题评阅记分)
(考生注意:只能从下列A、B、C三题中选做一题,如果多做,则按第一题评阅记分) ),B(x2,
),B(x2, )(x1<x2),坐标原点为O,△AOB的面积为S.
)(x1<x2),坐标原点为O,△AOB的面积为S.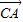 与
与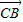 的夹角.
的夹角.