Question

（2012•韶关二模）在△ABC中，三个内角A，B，C的对边分别为a，b，c，其中c=2，且

cosA

cosB

=

b

a

=

3

1

．
（1）求证：△ABC是直角三角形；
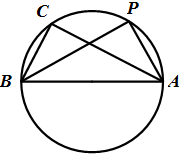
（2）如图，设圆O过A，B，C三点，点P位于劣弧

AC

上，求△PAC面积最大值．

Answer 1

分析：（1）由正弦定理求得sin2A=sin2B，故2A=2B或2A+2B=π，再由

b

a

=

3

1

，可得只能A+B=

π

2

，C=

π

2

，从而得到
△ABC是直角三角形．
（2）由（1）及c=2，及勾股定理得a=1，b=

3

，设∠PAB=θ(

π

6

＜θ＜

π

2

)，则 PA=AB•cosθ=2cosθ，化简△PAC面积为

3

2

sin(2θ-

π

6

) -

3

4

，再由θ的范围可得θ=

π

3

时，S_△PAC 取得最大值．

解答：（1）证明：由正弦定理得

cosA

cosB

=

sinB

sinA

，…（2分）
整理为sinAcosA=sinBcosB，即sin2A=sin2B，…（3分）
又因为0＜2A、2B＜2π，
∴2A=2B或2A+2B=π，即A=B或A+B=

π

2

．…（6分）
∵

b

a

=

3

1

，∴A=B舍去，故A+B=

π

2

，
由A+B=

π

2

可知C=

π

2

，∴△ABC是直角三角形．…（6分）
（2）解：由（1）及c=2，及勾股定理得a=1，b=

3

，…（7分）
设∠PAB=θ(

π

6

＜θ＜

π

2

)，则∠PAC=θ-

π

6

，…（8分）
在Rt△PAB中，PA=AB•cosθ=2cosθ
所以S△PAC=

1

2

PA•AC•sin(θ-

π

6

)=

1

2

•2•cosθ•

3

•sin(θ-

π

6

)=

3•

cosθ•sin(θ-

π

6

)…（10分）
=

3

cosθ(sinθ•

3

2

-cosθ•

1

2

)=

3

2

cosθsinθ-

3

2

cos2θ
=

3

4

sin2θ-

3

2

×

1+cos2θ

2

=

3

2

(

3

2

sin2θ-

1

2

cos2θ)-

3

4

=

3

2

sin(2θ-

π

6

)-

3

4

…（12分）
因为

π

6

＜θ＜

π

2

所以

π

6

＜2θ-

π

6

＜

5π

6

，
当2θ-

π

6

=

π

2

，即θ=

π

3

时，S_△PAC最大值等于

3

4

．…（14分）

点评：本题主要考查三角函数的恒等变换及化简求值，正弦定理、正弦函数的定义域和值域，属于中档题．