题目内容
10.若定义域为R的函数y=f(x),其图象是连续不断的,且存在常数λ(λ∈R),使得f(x+λ)+λf(x)=0对任意实数x都成立,则称f(x)是一个“λ-伴随函数”.给出下列四个关于“λ-伴随函数”的命题:①f(x)=0是常数函数中唯一一个“λ-伴随函数”;②f(x)=x+1是“λ-伴随函数”;③f(x)=2x是“λ-伴随函数”;④当λ>0时,“λ-伴随函数”f(x)在(0,λ)内至少有一个零点.所有真命题的序号为③.分析 假设函数为λ-伴随函数,根据定义得出f(x+λ)+λf(x)=0恒成立,从而得出λ的方程,根据方程是否有解得出假设是否成立.
解答 解:对于①,假设常数函数f(x)=k为λ-伴随函数”,则k+λk=0,∴(1+λ)k=0,
∴当λ=-1或k=0.
∴任意一个常数函数都是''λ-伴随函数'',其中λ=-1.
故①错误;
对于②,假设f(x)=x+1是“λ-伴随函数”,则x+λ+1+λ(x+1)=0恒成立,
即(1+λ)x+2λ+1=0恒成立,
∴$\left\{\begin{array}{l}{1+λ=0}\\{2λ+1=0}\end{array}\right.$,无解,故f(x)=x+1不是“λ-伴随函数”,
故②错误;
对于③,假设f(x)=2x是“λ-伴随函数”,则2x+λ+λ•2x=0恒成立,
即(2λ+λ)•2x=0恒成立,
∴2λ+λ=0,
做出y=2x和y=-x的函数图象如图: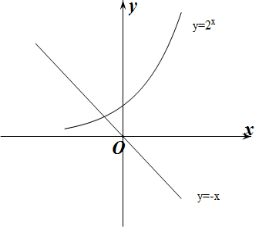
由图象可知方程2λ+λ=0有解,即f(x)=x+1是“λ-伴随函数”,
故③正确;
对于④,∵f(x)是“λ-伴随函数”,∴f(x+λ)+λf(x)=0恒成立,
∴f(λ)+λf(0)=0,
∴f(0)f(λ)+λf2(0)=0,即f(0)•f(λ)=-λ2f(0)≤0.
若f(0)≠0,则f(0)•f(λ)<0,∴f(x)在(0,λ)上至少存在一个零点,
若f(0)=0,则f(0)•f(λ)=0,则f(x)在(0,λ)上可能存在零点,也可能不存在零点.
故④错误.
故答案为③.
点评 本题考查了新定义的理解,函数恒成立问题的研究,方程根的存在性判断,属于中档题.

练习册系列答案
相关题目
5.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点F(-c,0)(c>0)作圆${x^2}+{y^2}=\frac{a^2}{4}$的切线,切点为E,延长FE交双曲线右支于点P.若$\overrightarrow{OP}=2\overrightarrow{OE}-\overrightarrow{OF}$,则双曲线的渐近线方程为( )
| A. | $\sqrt{10}x±2y=0$ | B. | $2x±\sqrt{10}y=0$ | C. | $\sqrt{6}x±2y=0$ | D. | $2x±\sqrt{6}y=0$ |
15.在△ABC中,$AB=3,AC=2,\overrightarrow{BD}=\frac{1}{2}\overrightarrow{BC},则\overrightarrow{AD}•\overrightarrow{DB}$的值为( )
| A. | $\frac{5}{2}$ | B. | $-\frac{5}{2}$ | C. | $\frac{5}{4}$ | D. | $-\frac{5}{4}$ |
19.(x2-x+y)5的展开式中,x4y3的系数为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
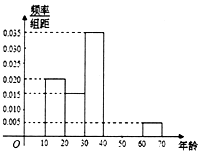 2017年由央视举办的一档文化益智节目《中国诗词大会》深受观众喜爱,某记者调查了部分年龄在[10,70]的观众,得到如下频率分布直方图.若第四、五、六组的人数依次成等差数列,且第六组有4人.
2017年由央视举办的一档文化益智节目《中国诗词大会》深受观众喜爱,某记者调查了部分年龄在[10,70]的观众,得到如下频率分布直方图.若第四、五、六组的人数依次成等差数列,且第六组有4人.