题目内容
1．一个等比数列共有3m项，若前2m项和为15，后2m项之和为60，则中间m项的和为12．分析 首先利用等比数列的前n项和公式求出S2m=15，S3m-Sm=60，即可求出qm，再根据S2m，求出中间m项的和．
解答 解：S2m=$\frac{{a}_{1}（1-{q}^{2m}）}{1-q}$=15
S3m-Sm=$\frac{{a}_{1}（{q}^{m}-{q}^{3m}）}{1-q}$=60，
解得qm=4，S2m=15=$\frac{{a}_{1}（1-{q}^{2m}）}{1-q}$=（1+qm）Sm=5Sm
∴Sm=$\frac{15}{5}$=3，中间n项为15-3=12．
故答案为：12．
点评 本题考查了等比数列的性质以及前n项和公式，要注意认真计算，属于中档题．
练习册系列答案
53随堂测系列答案
相关题目
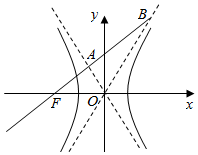如图，已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的左焦点为F，过F作斜率为1的直线交双曲线的渐近线于A，B两点，且|OB|=2|OA|，则该双曲线的离心率为$\sqrt{10}$．
20．若直线经过抛物线y2=4x的焦点且与抛物线相交于M、N两点，且线段MN中点的横坐标为3，则线段MN的长为（ ）
| A． | $\sqrt{13}$ | B． | 8 | C． | $8\sqrt{2}$ | D． | 16 |