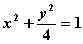题目内容
设椭圆的方程为 ,斜率为1的直线不经
,斜率为1的直线不经
过原点 ,而且与椭圆相交于
,而且与椭圆相交于 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)问:直线 与
与 能否垂直?若能,
能否垂直?若能, 之间满足什么关系;若不能,说明理由;
之间满足什么关系;若不能,说明理由;
(2)已知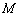 为
为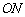 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若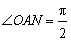 ,求椭圆的离心率.
,求椭圆的离心率.
解答:(1)∵斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于 两点,
两点,
∴可以设直线 的方程为
的方程为 .
.
∵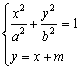 ,∴
,∴ ,
,
∴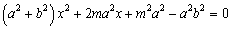 . ① ………………………………1分
. ① ………………………………1分
∵直线 与椭圆相交于
与椭圆相交于 两点,∴
两点,∴

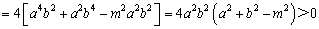 . ② …………………… 2分
. ② …………………… 2分
且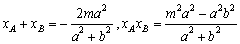 . ③ ……………………………… 3分
. ③ ……………………………… 3分
∵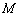 为线段
为线段 的中点,∴
的中点,∴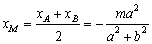 ,
,
∴ ,∴
,∴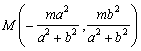 . ……… 4分
. ……… 4分
假设直线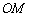 与
与 能垂直.
能垂直.
∵直线 的斜率为1,∴直线
的斜率为1,∴直线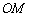 的斜率为-1,
的斜率为-1,
∴ ,∴
,∴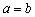 .……………………………………………… 5分
.……………………………………………… 5分
∵在椭圆方程 中,
中,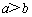 ,
,
∴假设不正确,在椭圆中直线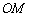 与
与 不能垂直. …………………………… 6分
不能垂直. …………………………… 6分
(2)∵M为ON的中点,M为AB的中点,∴四边形OANB为平行四边形.
∵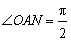 ,∴四边形OANB为矩形,∴
,∴四边形OANB为矩形,∴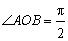 ,……………………… 7分
,……………………… 7分
∴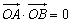 ,∴
,∴ ,∴
,∴ ,
,
∴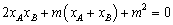 ,
,
∴ ,整理得
,整理得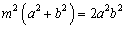 .……… 8分
.……… 8分
∵ 点在椭圆上,∴
点在椭圆上,∴ ,∴
,∴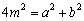 . …… 9分
. …… 9分
此时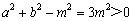 ,满足
,满足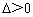 ,
,
消去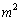 得
得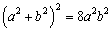 ,即
,即 . ………………………… 10分
. ………………………… 10分
设椭圆的离心率为e,则 ,∴
,∴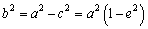 ,
,
∴ ,∴
,∴ ,
,
∴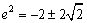 ,∵
,∵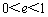 ,∴
,∴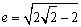 .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
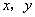 满足
满足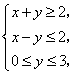 则
则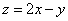 的最小值是( )
的最小值是( )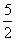 (C)
(C) (D)
(D)
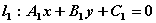 ,
,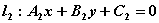 垂直的充要条件是
垂直的充要条件是 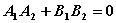 B、
B、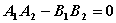 C、
C、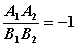 D、
D、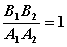
 是O为△BCD
是O为△BCD 的一元二次不等式
的一元二次不等式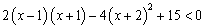 .
.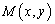 到两个定点
到两个定点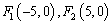 的距离之差的绝对值等于8,则动点M的轨迹方程为 ( )
的距离之差的绝对值等于8,则动点M的轨迹方程为 ( )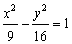 B.
B.
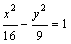 D.
D.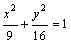
 B.
B.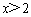
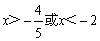 D.
D.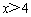
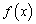 是奇函数,
是奇函数,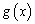 是偶函数,且满足
是偶函数,且满足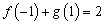 ,
,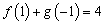 ,则
,则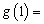 ( )
( ) 4 B.3 C.2 D.1
4 B.3 C.2 D.1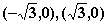 ,离心率是
,离心率是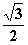 ,则椭圆C的方程为 ( ).
,则椭圆C的方程为 ( ).
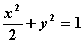 B.
B.  C.
C. 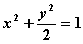 D.
D.