题目内容
若0＜a＜1，函数f（x）=|logax|，m=f(
)，n=f(
)，p=f(3)，则（ ）
| 1 |
| 4 |
| 1 |
| 2 |
| A、m＞n＞p |
| B、m＞p＞n |
| C、n＞m＞p |
| D、p＞m＞n |
分析：根据函数f（x）=|logax|得知：m=|loga4|，n=|loga2|，由图知函数在x＞1时为单调增函数，由于4＞3＞2，故而m＞p＞n
解答：
解：∵f（x）=|logax|，m=f(
)，n=f(
)
∴m=|loga4|，n=|loga2|
由图可知：函数在x＞1时为单调增函数
∵4＞3＞2
∴m＞p＞n
故选B
解：∵f（x）=|logax|，m=f(| 1 |
| 4 |
| 1 |
| 2 |
∴m=|loga4|，n=|loga2|
由图可知：函数在x＞1时为单调增函数
∵4＞3＞2
∴m＞p＞n
故选B
点评：本题考查了绝对值函数的图象，对绝对值里面的数进行讨论即可去掉绝对值，画出函数的图象，利用数形结合的思想即可解题，属于基础题．
练习册系列答案
相关题目
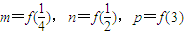，则（ ）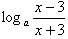
，g（x）=1+loga（x-1），设f（x），g（x）的定义域的公共部分为D，当[m，n]
D（m＜n）时，f（x）在[m，n]上的值域是[g（n），g（m）]，求a的取值范围。