题目内容
(本小题共14分)
设函数![]() 。
。
(Ⅰ)若曲线![]() 在点
在点![]() 处与直线
处与直线![]() 相切,求
相切,求![]() 的值;
的值;
(Ⅱ)求函数![]() 的单调区间与极值点。
的单调区间与极值点。
(Ⅰ)a,b分别为4和24
(Ⅱ)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,此时函数
上单调递增,此时函数![]() 没有极值点。
没有极值点。
当![]() 时,
时,
当![]() 时,函数
时,函数![]() 单调递增,
单调递增,
当![]() 时,函数
时,函数![]() 单调递减,
单调递减,
当![]() 时,函数
时,函数![]() 单调递增,
单调递增,
此时![]() 是
是![]() 的极大值点,
的极大值点,![]() 是
是![]() 的极小值点。
的极小值点。
解析:
本题主要考查利用导数研究函数的单调性和极值、解不等式等基础知识,考查综合分析和解决问题的能力。
(Ⅰ)![]() ,
,
∵曲线![]() 在点
在点![]() 处与直线
处与直线![]() 相切,
相切,
∴
(Ⅱ)∵![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,
此时函数![]() 没有极值点。
没有极值点。
当![]() 时,由
时,由![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
∴此时![]() 是
是![]() 的极大值点,
的极大值点,![]() 是
是![]() 的极小值点。
的极小值点。

练习册系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是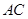 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.