题目内容
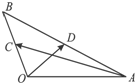如图，在△OAB中，∠AOB=120°，OA=2，OB=1，C、D分别是线段OB和AB的中点，那么| OD |
| AC |
-
| 3 |
| 2 |
-
．| 3 |
| 2 |
分析：由平面向量基本定理向量
，
来表示向量已知向量，由数量积的运算可得．
| OA |
| OB |
解答：解：由题意可得
•
=
(
+
)•
(
+
)
=
(
+
)•
(-
+
-
)
=
(
+
)•(-2
+
)
=
（-2
2-
•
+
2）
=
（-2×22-2×1×cos120°+12）
=-
故答案为：-
| OD |
| AC |
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 2 |
| AO |
| AB |
=
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 2 |
| OA |
| OB |
| OA |
=
| 1 |
| 4 |
| OA |
| OB |
| OA |
| OB |
=
| 1 |
| 4 |
| OA |
| OA |
| OB |
| OB |
=
| 1 |
| 4 |
=-
| 3 |
| 2 |
故答案为：-
| 3 |
| 2 |
点评：本题考查平面向量数量积的运算，用向量
，
来表示向量是解决问题的关键，属中档题．
| OA |
| OB |
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
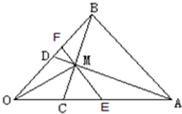如图，在△OAB中，
（2013•杭州二模）如图，在△OAB中，C为OA上的一点，且
如图，在△OAB中，已知
如图，在△OAB中，延长BA到C，使AC=BA，在OB上取点D，使DB=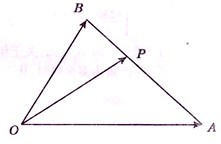
如图，在△OAB中，已知P为线段AB上的一点，且|