题目内容
设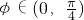 ,函数f(x)=sin2(x+φ),且
,函数f(x)=sin2(x+φ),且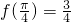 .
.
(Ⅰ)求φ的值;
(Ⅱ)若 ,求f(x)的最大值及相应的x值.
,求f(x)的最大值及相应的x值.
(Ⅰ)解:∵ ,∴
,∴ (4分)
(4分)
∵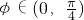 ,∴
,∴ ,∴
,∴ .(6分)
.(6分)
(Ⅱ)解:由(Ⅰ)得 (8分)
(8分)
∵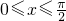 ,∴
,∴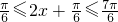 (9分)
(9分)
当 ,即
,即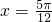 时,
时, 取得最小值-1(11分)
取得最小值-1(11分)
∴f(x)在 上的最大值为1,此时
上的最大值为1,此时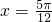 (12分)
(12分)
分析:(Ⅰ)把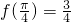 代入f(x)=sin2(x+φ),化简为
代入f(x)=sin2(x+φ),化简为 ,根据
,根据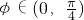 ,直接求出φ的值;
,直接求出φ的值;
(Ⅱ)化简函数的表达式为一个角的一个三角函数的形式,利用 ,求出相位的范围,即可求f(x)的最大值及相应的x值.
,求出相位的范围,即可求f(x)的最大值及相应的x值.
点评:本题是中档题,高考常考题,考查二倍角公式的应用,三角函数的最值等有关知识,整体思想的应用,掌握基本函数的基本性质是解好数学问题的前提,体现学生的数学解题素养.
 ,∴
,∴ (4分)
(4分)∵
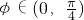 ,∴
,∴ ,∴
,∴ .(6分)
.(6分)(Ⅱ)解:由(Ⅰ)得
 (8分)
(8分)∵
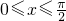 ,∴
,∴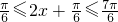 (9分)
(9分)当
 ,即
,即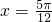 时,
时, 取得最小值-1(11分)
取得最小值-1(11分)∴f(x)在
 上的最大值为1,此时
上的最大值为1,此时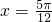 (12分)
(12分)分析:(Ⅰ)把
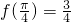 代入f(x)=sin2(x+φ),化简为
代入f(x)=sin2(x+φ),化简为 ,根据
,根据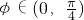 ,直接求出φ的值;
,直接求出φ的值;(Ⅱ)化简函数的表达式为一个角的一个三角函数的形式,利用
 ,求出相位的范围,即可求f(x)的最大值及相应的x值.
,求出相位的范围,即可求f(x)的最大值及相应的x值.点评:本题是中档题,高考常考题,考查二倍角公式的应用,三角函数的最值等有关知识,整体思想的应用,掌握基本函数的基本性质是解好数学问题的前提,体现学生的数学解题素养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 .
. 和
和 的值;
的值;
 ,数列{an}是等差数列吗?请给予证明;
,数列{an}是等差数列吗?请给予证明; (s=1,2,…).
(s=1,2,…). .
. 和
和 的值;
的值;
 ,数列{an}是等差数列吗?请给予证明;
,数列{an}是等差数列吗?请给予证明; (s=1,2,…).
(s=1,2,…).