题目内容
(2012•广东模拟)设奇函数f(x)对任意x∈R都有f(x)=f(x-1)+
.
(1)求f(
)和f(
)+f(
)(k=0,1,2,…,n)的值;
(2)数列{an}满足:an=f(0)+f(
)+f(
)+…+f(
)+f(1)-f(
),数列{an}是等差数列吗?请给予证明;
(3)设m与k为两个给定的不同的正整数,{an}是满足(2)中条件的数列,
证明:
|
-
|<(
)2|
-
|(s=1,2,…).
| 1 |
| 2 |
(1)求f(
| 1 |
| 2 |
| k |
| n |
| n-k |
| n |
(2)数列{an}满足:an=f(0)+f(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| 2 |
(3)设m与k为两个给定的不同的正整数,{an}是满足(2)中条件的数列,
证明:
| s |
 |
| n=1 |
| (m+1)nan+1 |
| (kn+n+k+1)an |
| s+1 |
| 2 |
| m |
| k |
分析:(1)直接根据f(x)=f(x-1)+
,且f(x)是奇函数把
代入即可求出f(
);再结合奇函数得到f(x)+f(1-x)=
;把x=
代入即可得到f(
)+f(
)(k=0,1,2,…,n)的值;
(2)先设sn=f(0)+f(
)+…+f(
)+f(1),利用倒序相加法结合第一问的结论,求出sn=
,进而求出数列{an}的通项公式,再根据定义即可证得数列{an}是等差数列;
(3)先根据第一问的结论把问题转化,再利用基本不等式对其放缩即可得到结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| n |
| k |
| n |
| n-k |
| n |
(2)先设sn=f(0)+f(
| 1 |
| n |
| n-1 |
| n |
| n+1 |
| 4 |
(3)先根据第一问的结论把问题转化,再利用基本不等式对其放缩即可得到结论.
解答:解:(1)∵f(x)=f(x-1)+
,且f(x)是奇函数
∴f(
)=f(
-1)+
=f(-
)+
=-f(
)+
∴2f(
)=
,故f(
)=
…(2分)
因为f(x)=f(x-1)+
=-f(1-x)+
,所以f(x)+f(1-x)=
.
令x=
,得f(
)+f(1-
)=
,即f(
)+f(
)=
.…(4分)
(2)设sn=f(0)+f(
)+…+f(
)+f(1)
又sn=f(1)+f(
)+…+f(
)+f(0)
两式相加2sn=[f(0)+f(1)]+[f(
)+f(
)]+…+[f(1)+f(0)]=
.
所以sn=
,…(6分)
故an=sn-f(
)=
-
=
,n∈N*…(7分)
又an+1-an=
-
=
.故数列{an}是等差数列.…(8分)
(3)∵
|
-
|
=
|
-
|
=
|
-
|
要证:
|
-
|<(
)2|
-
|(s=1,2,…)
即
|
-
|
<(
)2|
-
|…(10分)
∵
<
=
∴
+
+…+
<
+
+…+
=
=
<
即
<
,从而
<(
)2…(12分)
又∵|
-
|<|
-
|恒成立,
所以有
|
-
|
<(
)2|
-
|恒成立
即
|
-
|<(
)2|
-
|(s=1,2,…)…(14分)
| 1 |
| 2 |
∴f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴2f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
因为f(x)=f(x-1)+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令x=
| k |
| n |
| k |
| n |
| k |
| n |
| 1 |
| 2 |
| k |
| n |
| n-k |
| n |
| 1 |
| 2 |
(2)设sn=f(0)+f(
| 1 |
| n |
| n-1 |
| n |
又sn=f(1)+f(
| n-1 |
| n |
| 1 |
| n |
两式相加2sn=[f(0)+f(1)]+[f(
| 1 |
| n |
| n-1 |
| n |
| n+1 |
| 2 |
所以sn=
| n+1 |
| 4 |
故an=sn-f(
| 1 |
| 2 |
| n+1 |
| 4 |
| 1 |
| 4 |
| n |
| 4 |
又an+1-an=
| n+1 |
| 4 |
| n |
| 4 |
| 1 |
| 4 |
(3)∵
| s |
 |
| n=1 |
| (m+1)nan+1 |
| (kn+n+k+1)an |
=
| s |
 |
| n=1 |
(m+1)n
|
(k+1)(n+1)
|
=
| 1 |
| 2 |
| m+1 |
| k+1 |
| s |
 |
| n=1 |
| n(n+1) |
要证:
| s |
 |
| n=1 |
| (m+1)nan+1 |
| (kn+n+k+1)an |
| s+1 |
| 2 |
| m |
| k |
即
| 1 |
| 2 |
| m+1 |
| k+1 |
| s |
 |
| n=1 |
| n(n+1) |
| s+1 |
| 2 |
| m |
| k |
∵
| n×(n+1) |
| n+n+1 |
| 2 |
| 2n+1 |
| 2 |
∴
| 1×2 |
| 2×3 |
| s×(s+1) |
| 3 |
| 2 |
| 5 |
| 2 |
| 2s+1 |
| 2 |
| ||
| 2 |
| s2+2s |
| 2 |
| (s+1)2 |
| 2 |
即
| s |
 |
| n=1 |
| n(n+1) |
| (s+1)2 |
| 2 |
| 1 |
| 2 |
| s |
 |
| n=1 |
| n(n+1) |
| s+1 |
| 2 |
又∵|
| m+1 |
| k+1 |
| m |
| k |
所以有
| 1 |
| 2 |
| m+1 |
| k+1 |
| s |
 |
| n=1 |
| n(n+1) |
| s+1 |
| 2 |
| m |
| k |
即
| s |
 |
| n=1 |
| (m+1)nan+1 |
| (kn+n+k+1)an |
| s+1 |
| 2 |
| m |
| k |
点评:本题主要考察数列与不等式的综合问题.解决本题第一问的关键在于利用奇函数的性质得到f(x)+f(1-x)=
.而解决第二问的关键在于用到了倒序相加求和.
| 1 |
| 2 |

练习册系列答案
相关题目
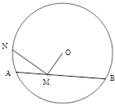 (2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=
(2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=