题目内容
3.直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=4,P为平面ABCD外一点,且PA=PB,PD=PC,N为CD中点.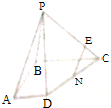
(1)求证:平面PCD⊥平面ABCD;
(2)在线段PC上是否存在一点E使得NE∥平面ABP.若存在,说明理由并确定E点的位置,若不存在请说明理由.
分析 (1)过P作PF⊥AB,垂足为F,利用等腰三角形的三线合一,首先判断AB⊥平面PNF,得到AB⊥PN,只要再判断PN与CD垂直即可;
(2)解:假设在线段PC上存在一点E使得NE∥平面ABP;由(1)得NF=3,并且NF∥BC,在平面PBC内,取CE=$\frac{1}{4}$PC,过E作EG∥BC,与PB交于G,判断四边形NEGF为平行四边形,得到线线平行,利用线面平行的判定定理可得.
解答 (1)证明:过P作PF⊥AB,垂足为F,∵PA=PB,∴F为AB 的中点,连接NF
∵N为CD中点,
∴PN⊥CD,NF∥BC,
∵AB⊥BC
∴NF⊥AB,
∴AB⊥平面PNF,
∴AB⊥PN,
∵AB,CD是梯形的两腰,即AB与CD相交,
∴PN⊥平面ABCD,
∵PN?平面PCD
∴平面PCD⊥平面ABCD;
(2)解:假设在线段PC上存在一点E使得NE∥平面ABP;由(1)得NF=3,并且NF∥BC,
在平面PBC内,取CE=$\frac{1}{4}$PC,过E作EG∥BC,与PB交于G,则EG=$\frac{3}{4}$BC=3,
∴NF∥EG,并且NF=EG,
∴四边形NEGF为平行四边形,
∴NE∥FG,
又NF?平面PAB,FG?平面PAB,
∴NE∥平面PAB.
所以在线段PC上存在一点E使得NE∥平面ABP.
点评 本题考查了面面垂直的判定定理的运用以及探索线面平行的条件,属于中档题.

练习册系列答案
相关题目
14.直线x+ay+1=0与圆x2+(y-1)2=4的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
11.如图,运行程序框图后输出S的值是( )

| A. | 0 | B. | $\frac{\sqrt{2}}{2}$+1 | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{2}}{2}$ |
12.设m=3${∫}_{-1}^{1}$(x2+sinx)}dx,则多项式(x+$\frac{1}{{m\sqrt{x}}}$)6的常数项为( )
| A. | $-\frac{5}{4}$ | B. | $\frac{5}{4}$ | C. | $-\frac{15}{16}$ | D. | $\frac{15}{16}$ |
