题目内容
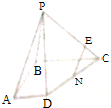
15.三棱锥P-ABC中,∠APB=∠BPC=∠CPA=60°,PA=a,PB=b,PC=c,求此三棱锥的体积.
分析 利用三面角公式求出PC与底面所成角的余弦函数值,然后求出C到底面的距离,底面PAB的面积,即可求解三棱锥的体积.
解答 解:由题意三棱锥P-ABC中,∠APB=∠BPC=∠CPA=60°,可知PC在底面PAB内的射影是∠BPA的平分线,
PC与∠BPA的平分线的夹角为θ,由三面角公式可得:cos60°=cos30°cosθ,
可得cosθ=$\frac{\sqrt{3}}{3}$.sinθ=$\frac{\sqrt{6}}{3}$.
C到底面PAB是距离为:PCsinθ=$\frac{\sqrt{6}}{3}$c.
底面PAB三角形的面积为:$\frac{1}{2}absin60°$=$\frac{\sqrt{3}}{4}ab$.
三棱锥的体积为:$\frac{1}{3}×\frac{\sqrt{3}}{4}ab×\frac{\sqrt{6}}{3}c$=$\frac{\sqrt{2}}{12}abc$.
点评 本题考查三面角公式的应用,几何体的体积的求法,考查计算能力以及空间想象能力.

练习册系列答案
相关题目
6.已知二次函数f(x)=ax2+bx+c满足:①f(3-x)=f(x);②f(1)=0;③对任意实数x,f(x)≥$\frac{1}{4a}$-$\frac{1}{2}$恒成立,求f(x)的解析式.
4.对于任意实数x,规定[x]表示不大于x的最大整数,则不等式4[x]2-12[x]+5<0成立的充分不必要条件是( )
| A. | x∈($\frac{1}{2}$,$\frac{5}{2}$) | B. | x∈($\frac{1}{2}$,3) | C. | x∈[1,2] | D. | x∈[1,3) |