题目内容
已知x=lnπ,y=log52,z=e-
,则x、y、z三者比较为
| 1 | 2 |
y<z<x
y<z<x
.分析:利用对数函数的单调性与性质以及指数函数的单调性与性质,推出x,y,z的范围,即可比较大小,得到答案.
解答:解:∵x=lnπ>lne=1,
0<log52<log5
=
,即y∈(0,
);
1=e0>e-
=
>
=
,即z∈(
,1),
∴y<z<x.
故答案为:y<z<x.
0<log52<log5
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
1=e0>e-
| 1 |
| 2 |
| 1 | ||
|
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
∴y<z<x.
故答案为:y<z<x.
点评:本题考查不等式比较大小,掌握对数函数与指数函数的性质是解决问题的关键,属于基础题.

练习册系列答案
相关题目
已知x=lnπ,y=log5
,z=e
,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、x>z>y |
| B、z<x<y |
| C、z<y<x |
| D、x<y<z |
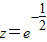 ,则( )
,则( ) ,则( )
,则( )