题目内容
2.已知函数f(x)=arcsin(2x+1)(-1≤x≤0),则f-1($\frac{π}{6}$)=-$\frac{1}{4}$.分析 由条件利用反正弦函数的定义,求得f-1($\frac{π}{6}$)的值,
解答 解:∵函数f(x)=arcsin(2x+1),-1≤x≤0,∴-1≤2x+1≤1,
∴f-1(x)=$\frac{sinx-1}{2}$,则f-1($\frac{π}{6}$)=$\frac{sin\frac{π}{6}-1}{2}$=-$\frac{1}{4}$,
故答案为:-$\frac{1}{4}$.
点评 本题主要考查反正弦函数的应用,属于基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
10.i是虚数单位,若复数z满足zi=-1+i,则复数z的实部与虚部的和是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
17.直线x+y+1=0与坐标轴围成的三角形的面积为( )
| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{1}{2}$ |
 如图,在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°.
如图,在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°. 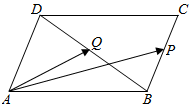 在边长为2的菱形ABCD中,∠BAD=60°,P,Q分别是BC,BD的中点,则向量$\overrightarrow{AP}$与$\overrightarrow{AQ}$的夹角的余弦值为$\frac{3\sqrt{21}}{14}$.
在边长为2的菱形ABCD中,∠BAD=60°,P,Q分别是BC,BD的中点,则向量$\overrightarrow{AP}$与$\overrightarrow{AQ}$的夹角的余弦值为$\frac{3\sqrt{21}}{14}$.