题目内容
用0,1,3,5,7五个数字,可以组成多少个没有重复数字且5不在十位位置上的五位数?
解 (1)符合要求的四位偶数可分为三类:
第一类:0在个位时有A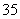 个;
个;
第二类:2在个位时,首位从1,3,4,5中选定1个(A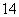 种),十位和百位从余下的数字中选(有A
种),十位和百位从余下的数字中选(有A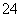 种),于是有A
种),于是有A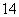 ·A
·A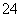 个;
个;
第三类:4在个位时,与第二类同理,也有A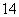 ·A
·A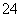 个.
个.
由分类计数原理知,共有四位偶数为A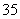 +A
+A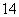 ·A
·A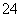 +A
+A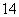 ·A
·A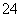 =156(个).
=156(个).
( 2)五位
2)五位 数中5的倍数的数可分为两类:个位数字是0的五位数是A
数中5的倍数的数可分为两类:个位数字是0的五位数是A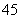 个;个位数字是5的五位数有A
个;个位数字是5的五位数有A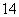 ·A
·A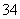 个.
个.
故满足条件的五位数共有A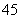 +A
+A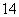 ·A
·A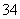 =216(个).
=216(个).
(3)比1 325大的四位数可分为三类:
第一类:形如2□□□,3□□□,4□□□,5□□□,共有A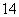 ·A
·A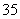 个
个 ;
;
第二类:形如14□□,15□□,共有A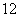 ·A
·A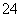 个;
个;
第三类:形如134□,13 5□,共有A
5□,共有A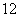 ·A
·A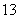 个.
个.
由分类计数原理知,比1 325大 的四位数共有
的四位数共有
 =270(个).
=270(个).

练习册系列答案
相关题目
 ,则该线性方程组的解是
,则该线性方程组的解是 

 欢乐今宵”节目中拿出两个信箱,其中存放着先后两
欢乐今宵”节目中拿出两个信箱,其中存放着先后两 次竞猜中成绩优秀的观众来信
次竞猜中成绩优秀的观众来信 动员10人,3人会划右舷,2人会划左舷,其余5人两舷都能划,现要从中选6人上艇,平均分配在两舷上划浆,有多少种不同的选法?
动员10人,3人会划右舷,2人会划左舷,其余5人两舷都能划,现要从中选6人上艇,平均分配在两舷上划浆,有多少种不同的选法?