题目内容
4.已知集合A={-1,3,4},B={0,1,4,5},则A∩B子集的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 先求出A∩B,从而求出其子集的个数.
解答 解:∵集合A={-1,3,4},B={0,1,4,5},
∴A∩B={4},
故其子集的个数为2个,
故选:C.
点评 本题考察了交集的运算,考察集合的子集问题,是一道基础题.

练习册系列答案
相关题目
1.长方体的相邻三个面的面积分别是12,15,20,且它的八个顶点都在同一个球面上,这个球的表面积是( )
| A. | 100π | B. | 60π | C. | 50π | D. | 30π |
9.tan(-$\frac{4π}{3}$)+tan$\frac{4π}{3}$等于( )
| A. | -2$\sqrt{3}$ | B. | -$\frac{2\sqrt{3}}{3}$ | C. | 0 | D. | $\frac{2\sqrt{3}}{3}$ |
16.下列不等式中,正确的是( )
| A. | 0.8-0.1>0.8-0.2 | B. | log0.53>log0.52 | C. | sin$\frac{2π}{5}$<sin$\frac{π}{5}$ | D. | 0.7-0.3>0.82.2 |
13.已知O为坐标原点,$\overrightarrow{OA}$=(1,2),$\overrightarrow{OB}$=(-2,-1),则$\frac{|\overrightarrow{AB}|}{\overrightarrow{OA}•\overrightarrow{OB}}$=( )
| A. | -$\frac{3\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | -$\frac{3\sqrt{2}}{4}$ | D. | $\frac{3\sqrt{2}}{4}$ |
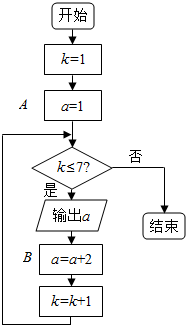 按图所示的程序框图操作:
按图所示的程序框图操作: