题目内容
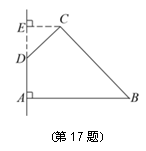
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2![]() ,AD=2,求四边形ABCD绕直线AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕直线AD旋转一周所成几何体的表面积及体积.
 |
解:S表面=S下底面+S台侧![]() 面+S锥侧面
面+S锥侧面
=×52+×(2+5)×5+×2×2![]() =(60+4
=(60+4![]() ).
).
V=V台-V锥=![]() (
(![]() +r1r2+
+r1r2+![]() )h-
)h-![]() r2h1=
r2h1=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2![]() ,AD=2,求四边形ABCD绕直线AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕直线AD旋转一周所成几何体的表面积及体积.
 |
解:S表面=S下底面+S台侧![]() 面+S锥侧面
面+S锥侧面
=×52+×(2+5)×5+×2×2![]() =(60+4
=(60+4![]() ).
).
V=V台-V锥=![]() (
(![]() +r1r2+
+r1r2+![]() )h-
)h-![]() r2h1=
r2h1=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案