题目内容
本小题满分12分)
如图点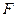 为双曲线
为双曲线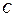 的左焦点,左准线
的左焦点,左准线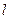 交
交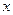 轴于点
轴于点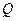 ,点P是
,点P是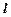 上的一点
上的一点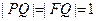 ,且线段PF的中点
,且线段PF的中点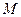 在双曲线
在双曲线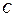 的左支上.
的左支上.
(1)求双曲线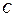 的标准方程;
的标准方程;
(2)若过点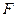 的直线
的直线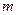 与双曲线
与双曲线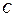 的左右两支分别交于
的左右两支分别交于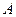 、
、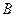 两点,设
两点,设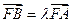 ,当
,当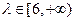 时,求直线
时,求直线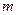 的斜率
的斜率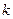 的取值范围.
的取值范围.
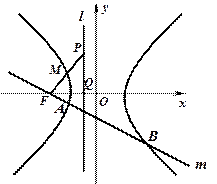
如图点
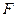 为双曲线
为双曲线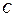 的左焦点,左准线
的左焦点,左准线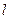 交
交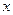 轴于点
轴于点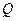 ,点P是
,点P是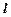 上的一点
上的一点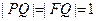 ,且线段PF的中点
,且线段PF的中点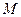 在双曲线
在双曲线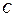 的左支上.
的左支上.(1)求双曲线
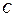 的标准方程;
的标准方程;(2)若过点
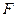 的直线
的直线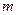 与双曲线
与双曲线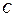 的左右两支分别交于
的左右两支分别交于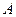 、
、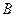 两点,设
两点,设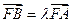 ,当
,当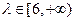 时,求直线
时,求直线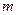 的斜率
的斜率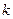 的取值范围.
的取值范围. 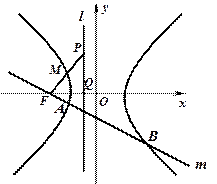
解:(Ⅰ)设双曲线方程为 (
( ,
, ),
),
则 ,
, ,∴
,∴ .------------------------(2分)
.------------------------(2分)
又 在双曲线上,∴
在双曲线上,∴ .
.
联立①②③,解得 ,
, .∴双曲线方程为
.∴双曲线方程为 .--------(4分)
.--------(4分)
注:对点M用第二定义,得 ,可简化计算.
,可简化计算.
(Ⅱ) ,设
,设 ,
, ,m:
,m: ,则
,则
由 ,得
,得 ,
, .--------------------(6分)
.--------------------(6分)
由 ,得
,得 .
.
∴ ,
, .
. .
.
由 ,
, ,
, ,---------------------(8分)
,---------------------(8分)
消去 ,
, ,
,
得 .------------------------(9分)
.------------------------(9分)
∵ ,函数
,函数 在
在 上单调递增,
上单调递增,
∴ ,∴
,∴ .------------------------(10分)
.------------------------(10分)
又直线m与双曲线的两支相交,即方程 两根同号,
两根同号,
∴ .------------------------------------------------(11分)
.------------------------------------------------(11分)
∴ ,故
,故 .------------------------(12分)
.------------------------(12分)
 (
( ,
, ),
),则
 ,
, ,∴
,∴ .------------------------(2分)
.------------------------(2分)又
 在双曲线上,∴
在双曲线上,∴ .
.联立①②③,解得
 ,
, .∴双曲线方程为
.∴双曲线方程为 .--------(4分)
.--------(4分)注:对点M用第二定义,得
 ,可简化计算.
,可简化计算.(Ⅱ)
 ,设
,设 ,
, ,m:
,m: ,则
,则由
 ,得
,得 ,
, .--------------------(6分)
.--------------------(6分)由
 ,得
,得 .
.∴
 ,
, .
. .
.由
 ,
, ,
, ,---------------------(8分)
,---------------------(8分)消去
 ,
, ,
,得
 .------------------------(9分)
.------------------------(9分)∵
 ,函数
,函数 在
在 上单调递增,
上单调递增,∴
 ,∴
,∴ .------------------------(10分)
.------------------------(10分)又直线m与双曲线的两支相交,即方程
 两根同号,
两根同号,∴
 .------------------------------------------------(11分)
.------------------------------------------------(11分)∴
 ,故
,故 .------------------------(12分)
.------------------------(12分)略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 (1,0),点
(1,0),点 .Q在双曲线的右支上,点
.Q在双曲线的右支上,点 (
( ,0)到直线
,0)到直线 的距离为1.
的距离为1. 且有
且有 ,求实数
,求实数 时,
时,
 的内心恰好是点
的内心恰好是点 =1相交于两个不同的点A、B。
=1相交于两个不同的点A、B。 x轴上的点M(3,0)到A、B两点的距离相等,求k的值。
x轴上的点M(3,0)到A、B两点的距离相等,求k的值。 -
- =1的渐近线与圆
=1的渐近线与圆 相切,则此双曲线的离心率为 ▲ .
相切,则此双曲线的离心率为 ▲ .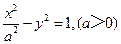 的一条准线方程为
的一条准线方程为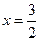 ,则其离心率为 。
,则其离心率为 。 
 的左焦点为
的左焦点为 与
与 轴的交点为
轴的交点为 是双曲线右支上任意一点,则分别以线段
是双曲线右支上任意一点,则分别以线段 为直径的两圆位置关系为 ( )
为直径的两圆位置关系为 ( ) 相交
相交  相切
相切 
 相离
相离  以上情况都有可能
以上情况都有可能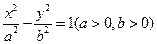 左支上一点,
左支上一点,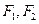 分别为双曲线的左、右焦点,若
分别为双曲线的左、右焦点,若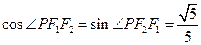 ,则此双曲线离心率是
,则此双曲线离心率是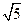
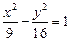 的渐近线方程为( )
的渐近线方程为( )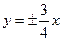
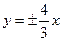
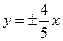

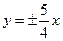
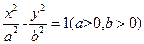 ,
,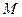 、
、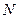 是双曲线上关于原点对称的两点,
是双曲线上关于原点对称的两点,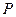 是双曲线上任意一点,且直线
是双曲线上任意一点,且直线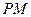 、
、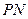 的斜率分别为
的斜率分别为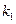 、
、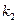 (
(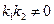 ),若
),若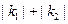 的最小值为1,则双曲线的离心率为 .
的最小值为1,则双曲线的离心率为 .