题目内容
(本小题满分14分)
设各项均为正数的数列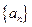 的前
的前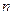 项和为
项和为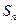 ,已知数列
,已知数列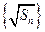 是首项为
是首项为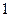 ,公差为
,公差为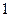 的等差
的等差
数列.
(1) 求数列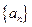 的通项公式;
的通项公式;
(2)令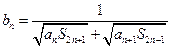 ,若不等式
,若不等式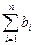
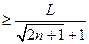 对任意
对任意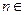 N
N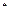 都成立,
都成立,
求实数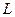 的取值范围.
的取值范围.
设各项均为正数的数列
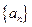 的前
的前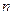 项和为
项和为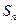 ,已知数列
,已知数列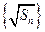 是首项为
是首项为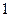 ,公差为
,公差为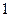 的等差
的等差数列.
(1) 求数列
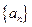 的通项公式;
的通项公式;(2)令
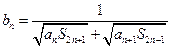 ,若不等式
,若不等式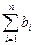
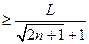 对任意
对任意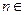 N
N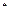 都成立,
都成立,求实数
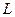 的取值范围.
的取值范围.(本小题满分14分)
(本小题主要考查数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)
(1)解:∵数列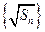 是首项为
是首项为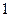 ,公差为
,公差为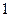 的等差数列,
的等差数列,
∴ .
.
∴ . …… 2分
. …… 2分
当 时,
时, ;
;
当
 时,
时,

 .
.
又 适合上式.
适合上式.
∴ . …… 4分
. …… 4分
(2)解: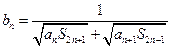



 . …… 6分
. …… 6分
∴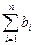



 . …… 8分
. …… 8分
故要使不等式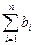
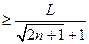 对任意
对任意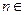 N
N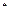 都成立,
都成立,
即
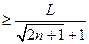 对任意
对任意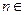 N
N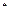 都成立,
都成立,
得 对任意
对任意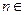 N
N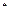 都成立. …… 10分
都成立. …… 10分
令 ,则
,则 .
.
∴ . ∴
. ∴ . …… 12分
. …… 12分
∴ .
.
∴实数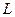 的取值范围为
的取值范围为 . …… 14分
. …… 14分
[另法]:

 .
.
∴ . ∴
. ∴ . …… 12分
. …… 12分
∴ .
.
∴实数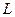 的取值范围为
的取值范围为 . …… 14分
. …… 14分
(本小题主要考查数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)
(1)解:∵数列
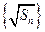 是首项为
是首项为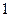 ,公差为
,公差为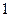 的等差数列,
的等差数列,∴
 .
.∴
 . …… 2分
. …… 2分当
 时,
时, ;
;当

 时,
时,

 .
.又
 适合上式.
适合上式.∴
 . …… 4分
. …… 4分(2)解:
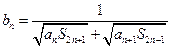



 . …… 6分
. …… 6分∴
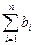



 . …… 8分
. …… 8分故要使不等式
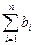
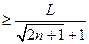 对任意
对任意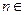 N
N 都成立,
都成立,即

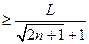 对任意
对任意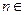 N
N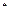 都成立,
都成立,得
 对任意
对任意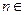 N
N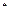 都成立. …… 10分
都成立. …… 10分令
 ,则
,则 .
.∴
 . ∴
. ∴ . …… 12分
. …… 12分∴
 .
.∴实数
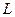 的取值范围为
的取值范围为 . …… 14分
. …… 14分[另法]:


 .
.∴
 . ∴
. ∴ . …… 12分
. …… 12分∴
 .
.∴实数
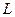 的取值范围为
的取值范围为 . …… 14分
. …… 14分略

练习册系列答案
相关题目


 的表达式.
的表达式. 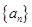 的公差大于0,且
的公差大于0,且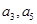 是方程
是方程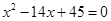 的两根,数列
的两根,数列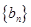 的前
的前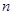 项的和为
项的和为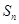 ,且
,且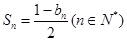 .
.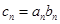 ,求数列
,求数列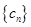 的前
的前 )是函数
)是函数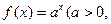 且
且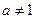 )的图象上一点,等比数列
)的图象上一点,等比数列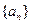 的前
的前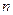 项和为
项和为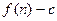 ,数列
,数列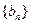
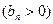 的首项为
的首项为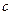 ,且前
,且前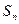 满足
满足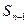 =
=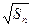 +
+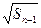 (
(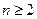 ).
).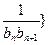 前
前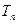 ,问
,问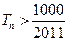 的最小正整数
的最小正整数
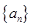 中,
中,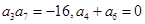 ,求
,求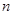 项和
项和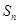 。
。 中,若
中,若 ,则前20项的和
,则前20项的和 等于( )
等于( ) (1,0)
(1,0) 共有
共有
 项,其中所有奇数项之和为310,所有偶数项之和为300,则
项,其中所有奇数项之和为310,所有偶数项之和为300,则 的值为 ( )
的值为 ( )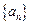 是等差数列,则通项为
是等差数列,则通项为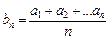 的
的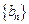 也是等差数列,类似上述命题,相应的等比数列有性质:若
也是等差数列,类似上述命题,相应的等比数列有性质:若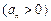 ,则通项为
,则通项为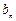 =__
=__ __________的数列
__________的数列