题目内容
.设数列
(1)求
(2)求 的表达式.
的表达式.

(1)求

|
 的表达式.
的表达式. 解:(1)当 时,由已知得
时,由已知得
同理,可解得 4分
4分
(2)解法一:由题设 当
当
代入上式,得 (*) 6分
(*) 6分
由(1)可得 由(*)式可得
由(*)式可得
由此猜想: 8分
8分
证明:①当 时,结论成立.②假设当
时,结论成立.②假设当 时结论成立,
时结论成立,
即 那么,由(*)得
那么,由(*)得

所以当 时结论也成立,根据①和②可知,
时结论也成立,根据①和②可知,
 对所有正整数n都成立.因
对所有正整数n都成立.因 12分
12分
解法二:由题设 当
当
代入上式,得


 -1的等差数列,
-1的等差数列,

 12分
12分
 时,由已知得
时,由已知得
同理,可解得
 4分
4分(2)解法一:由题设
 当
当
代入上式,得
 (*) 6分
(*) 6分由(1)可得
 由(*)式可得
由(*)式可得
由此猜想:
 8分
8分证明:①当
 时,结论成立.②假设当
时,结论成立.②假设当 时结论成立,
时结论成立,即
 那么,由(*)得
那么,由(*)得

所以当
 时结论也成立,根据①和②可知,
时结论也成立,根据①和②可知, 对所有正整数n都成立.因
对所有正整数n都成立.因 12分
12分解法二:由题设
 当
当
代入上式,得



 -1的等差数列,
-1的等差数列,
 12分
12分略

练习册系列答案
相关题目
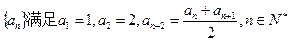
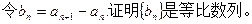
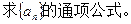
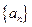 的前
的前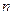 项和为
项和为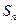 ,已知数列
,已知数列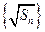 是首项为
是首项为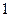 ,公差为
,公差为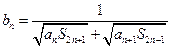 ,若不等式
,若不等式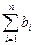
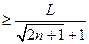 对任意
对任意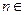 N
N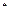 都成立,
都成立,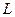 的取值范围.
的取值范围.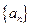 为等差数列,
为等差数列,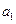 +
+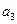 +
+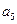 =105,
=105,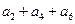 =99,以
=99,以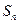 表示
表示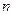 项和,则使得
项和,则使得 的前n项和为
的前n项和为 ,则( )
,则( )



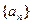 中,
中,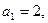 公积为5,当n为奇数时,这个数列的前
公积为5,当n为奇数时,这个数列的前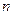 项和
项和 =_________。
=_________。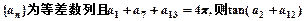 的值为 ( )
的值为 ( )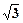
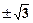
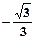
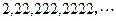 的一个通项公式
的一个通项公式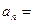 ______;
______; 中,
中,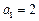 ,且有
,且有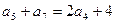 ,
, 则
则 ( )
( )