题目内容
 某个建筑物的墙面上,有如图所示的图案,现按同样的规律继续发展,设第n个图案包含f(n)个小图形,则f(5)=
某个建筑物的墙面上,有如图所示的图案,现按同样的规律继续发展,设第n个图案包含f(n)个小图形,则f(5)=考点:归纳推理
专题:规律型
分析:解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.
解答:
解:第一个图需1个小图形;
第二个图需6+1=7个小图形;
第三个图需2×6+6+1=19个小图形;
…
第n个图需6[1+2+3+…+(n-1)]+1=3n2-3n+1个小图形.
即f(n)=3n2-3n+1,
将n=5时,f(5)=61,
故答案为:61,3n2-3n+1.
第二个图需6+1=7个小图形;
第三个图需2×6+6+1=19个小图形;
…
第n个图需6[1+2+3+…+(n-1)]+1=3n2-3n+1个小图形.
即f(n)=3n2-3n+1,
将n=5时,f(5)=61,
故答案为:61,3n2-3n+1.
点评:此题考查了规律型中的图形变化问题,主要培养学生的观察能力和空间想象能力.

练习册系列答案
相关题目
已知函数f(x)=x3-tx2+3x,若对于任意的a∈[1,2],b∈(2,3],函数f(x)在区间(a,b)上单调递减,则实数t的取值范围是( )
| A、(-∞,3] |
| B、(-∞,5] |
| C、[3,+∞) |
| D、[5,+∞) |
下列函数中,在(0,+∞)上为减函数的是( )
A、y=
| ||
| B、y=(1-x)ex | ||
| C、y=x-ln(1+x) | ||
| D、y=x3-x |
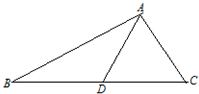 如图,在△ABC中,D是BC上的点,∠C=∠D=2∠DAB,△BAD的面积与△CAD的面积相等,且
如图,在△ABC中,D是BC上的点,∠C=∠D=2∠DAB,△BAD的面积与△CAD的面积相等,且